DW-Task03-偏差与方差理论
偏差与方差理论
优化基础模型
在刚刚的回归问题的基本算法中,我们使用数据集去估计模型的参数,如线性回归模型中的参数w,那么这个数据集我们称为训练数据集,简称训练集。我们在回归问题中使用训练集估计模型的参数的原则一般都是使得我们的损失函数在训练集达到最小值,其实在实际问题中我们是可以让损失函数在训练集最小化为0,如:在线性回归中,我加入非常多的高次项,使得我们模型在训练集的每一个数据点都恰好位于曲线上,那这时候模型在训练集的损失值也就是误差为0。
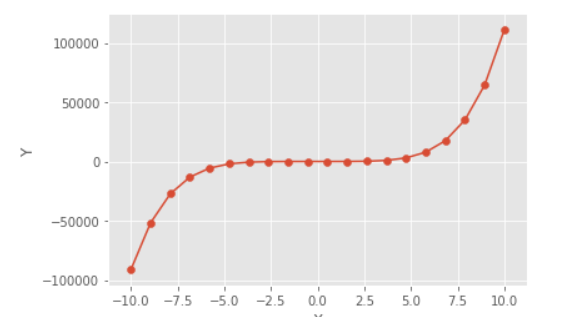
既然能做到这件事,是不是代表我们的建模完事大吉呢?换句话说我们的模型可以预测任意情况呢?答案是显然否定的。我们建立机器学习的目的并不是为了在已有的数据集,也就是训练集上效果表现非常优异,我们希望建立的机器学习模型在未知且情况复杂的测试数据上表现优异,我们称这样的未出现在训练集的未知数据集成为测试数据集,简称测试集。我们希望模型在测试集上表现优异!因为假如我们根据股票市场前六个月的数据拟合一个预测模型,我们的目的不是为了预测以前这六个月越准越好,而是预测明天乃至未来的股价变化。
(a) 训练均方误差与测试均方误差:
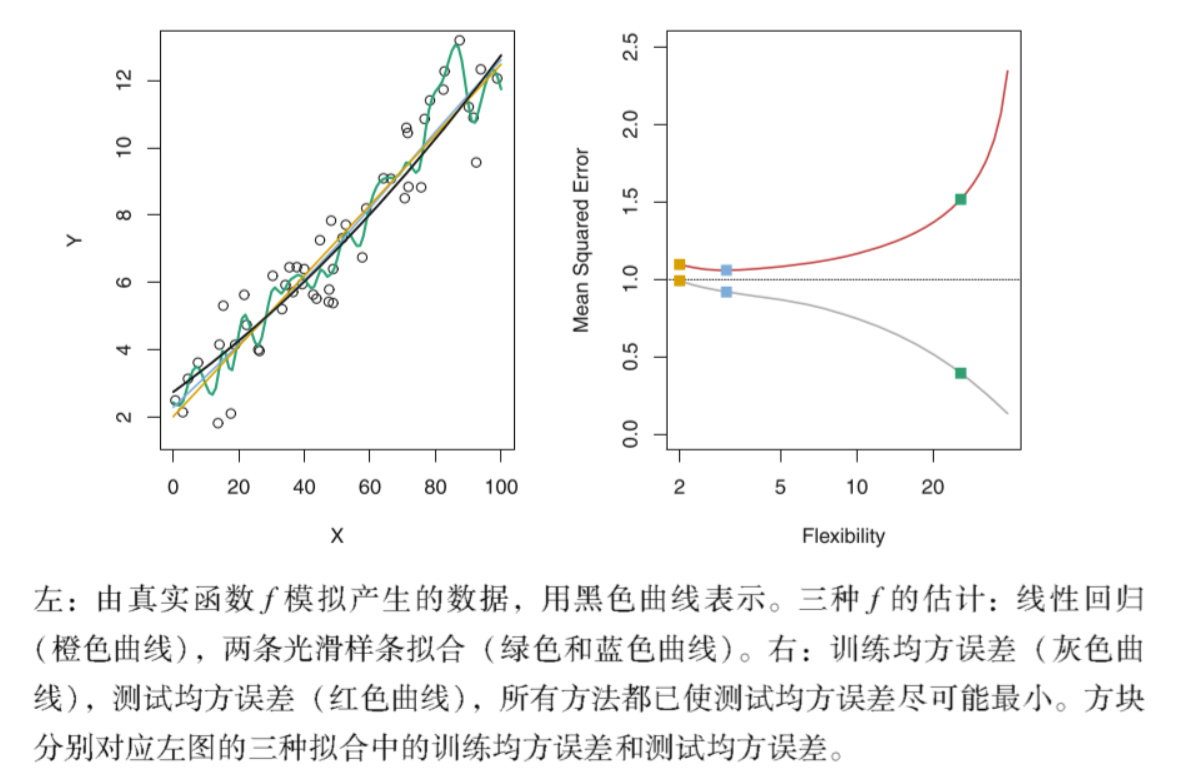
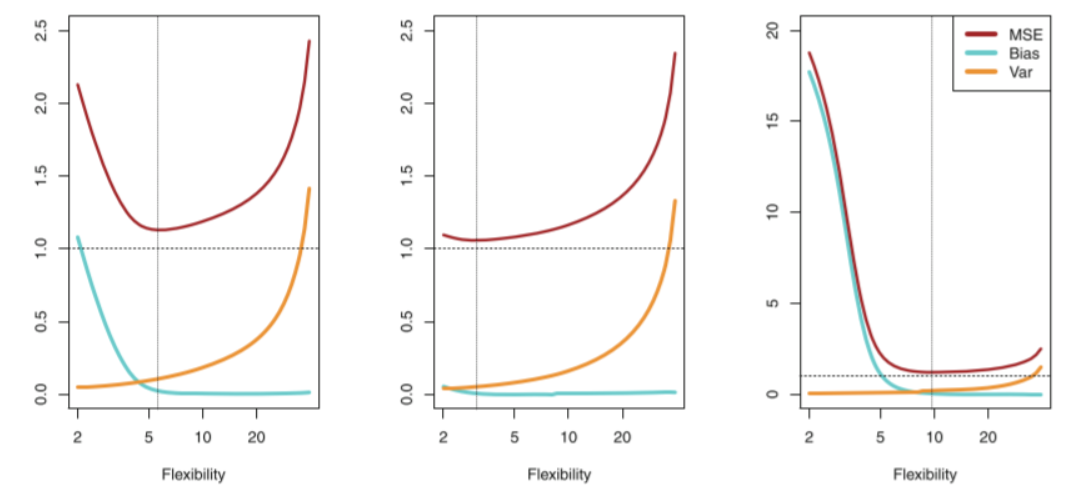
在回归中,我们最常用的评价指标为均方误差,即:$MSE = \frac{1}{N}\sum\limits_{i=1}^{N}(y_i -\hat{ f}(x_i))^2$,其中$\hat{ f}(x_i)$是样本$x_i$应用建立的模型$\hat{f}$预测的结果。如果我们所用的数据是训练集上的数据,那么这个误差为训练均方误差,如果我们使用测试集的数据计算的均方误差,我们称为测试均方误差。一般而言,我们并不关心模型在训练集上的训练均方误差,我们关心的是模型面对未知的样本集,即测试集上的测试误差,我们的目标是使得我们建立的模型在测试集上的测试误差最小。那我们如何选择一个测试误差最小的模型呢?这是个棘手的问题,因为在模型建立阶段,我们是不能得到测试数据的,比如:我们在模型未上线之前是不能拿到未知且真实的测试数据来验证我们的模型的。在这种情况下,为了简便起见,一些观点认为通过训练误差最小化来选择模型也是可行的。这种观点表面看上去是可行的,但是存在一个致命的缺点,那就是:一个模型的训练均方误差最小时,不能保证测试均方误差同时也很小。对于这种想法构造的模型,一般在训练误差达到最小时,测试均方误差一般很大!如图:
- 可以看到:当我们的模型的训练均方误差达到很小时,测试均方误差反而很大,但是我们寻找的最优的模型是测试均方误差达到最小时对应的模型,因此基于训练均方误差达到最小选择模型本质上是行不同的。正如上右图所示:模型在训练误差很小,但是测试均方误差很大时,我们称这种情况叫模型的过拟合。
(b) 偏差-方差的权衡:
从上图的测试均方误差曲线可以看到:测试均方误差曲线呈现U型曲线,这表明了在测试误差曲线中有两种力量在互相博弈。可以证明:
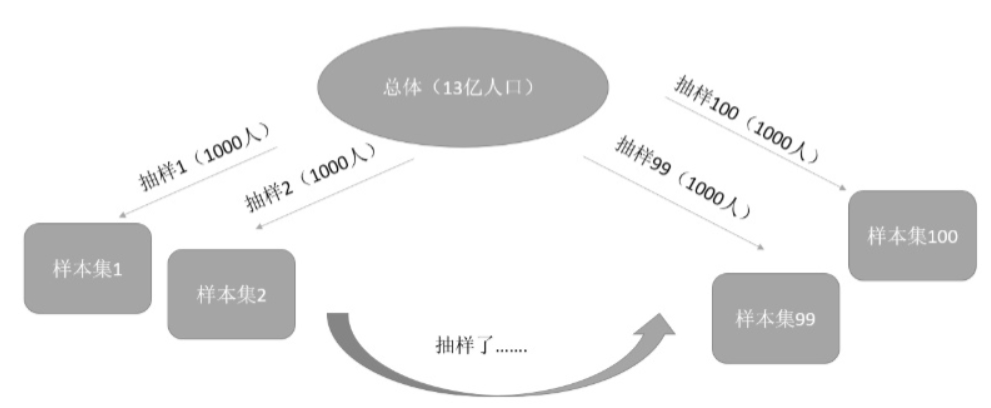
也就是说,我们的测试均方误差的期望值可以分解为$\hat{f}(x_0)$的方差、$\hat{f}(x_0)$的偏差平方和误差项$\epsilon$的方差。为了使得模型的测试均方误差达到最小值,也就是同时最小化偏差的平方和方差。由于我们知道偏差平方和方差本身是非负的,因此测试均方误差的期望不可能会低于误差的方差,因此我们称$\operatorname{Var}(\varepsilon)$为建模任务的难度,这个量在我们的任务确定后是无法改变的,也叫做不可约误差。那么模型的方差和偏差的平方和究竟是什么呢?所谓模型的方差就是:用不同的数据集去估计$f$时,估计函数的改变量。举个例子:我们想要建立一个线性回归模型,可以通过输入中国人身高去预测我们的体重。但是显然我们没有办法把全中国13亿人做一次人口普查,拿到13亿人的身高体重去建立模型。我们能做的就是从13亿中抽1000个样本进行建模,我们对这个抽样的过程重复100遍,就会得到100个1000人的样本集。我们使用线性回归模型估计参数就能得到100个线性回归模型。由于样本抽取具有随机性,我们得到的100个模型不可能参数完全一样,那么这100个模型之间的差异就叫做方差。显然,我们希望得到一个稳定的模型,也就是在不同的样本集估计的模型都不会相差太大,即要求f的方差越小越好。一般来说,模型的复杂度越高,f的方差就会越大。 如加入二次项的模型的方差比线性回归模型的方差要大。
另一方面,模型的偏差是指:为了选择一个简单的模型去估计真实函数所带入的误差。假如真实的数据X与Y的关系是二次关系,但是我们选择了线性模型进行建模,那由于模型的复杂度引起的这种误差我们称为偏差,它的构成时复杂的。偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。偏差度量的是单个模型的学习能力,而方差度量的是同一个模型在不同数据集上的稳定性。“偏差-方差分解”说明:泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小。
总的来说,偏差和方差是越小越好,越小的方差代表模型算法的稳定性和泛化能力较好,在不同的数据集合上得到的预测结果都较为稳定,不会出现差异过大的结果。越小的偏差代表模型在预测的准确度上表现得越好,即每每都能击中靶心。
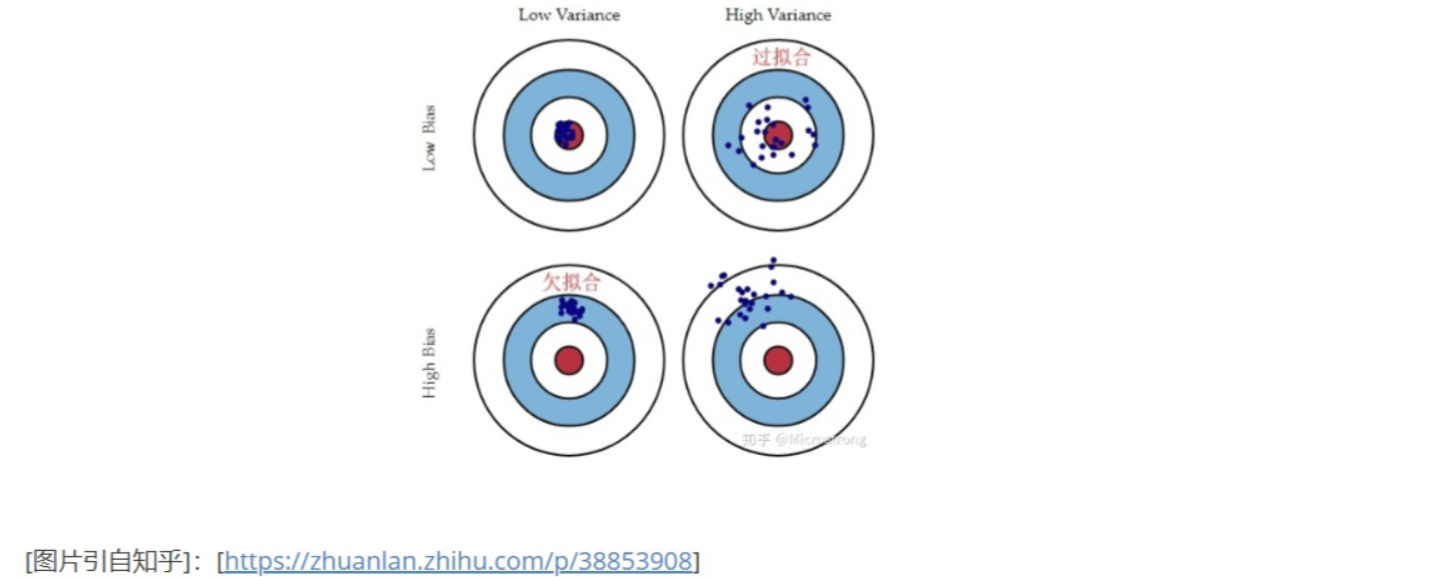
一般而言,增加模型的复杂度,会增加模型的方差,但是会减少模型的偏差,我们要找到一个方差—偏差的权衡,使得测试均方误差最小。
(c) 特征提取:
在前面的讨论中,我们已经明确一个目标,就是:我们要选择一个测试误差达到最小的模型。但是实际上我们很难对实际的测试误差做精确的计算,因此我们要对测试误差进行估计,估计的方式有两种:训练误差修正与交叉验证。
训练误差修正(补充):
根据前面的讨论我们已经知道,模型越复杂,训练误差越小,测试误差先减后增。因此,我们先构造一个特征较多的模型使其过拟合,此时训练误差很小而测试误差很大,那这时我们加入关于特征个数的惩罚。因此,当我们的训练误差随着特征个数的增加而减少时,惩罚项因为特征数量的增加而增大,抑制了训练误差随着特征个数的增加而无休止地减小。具体的数学量如下:
其中d为模型特征个数,
$\hat{\sigma}^2$为模型预测误差的方差的估计值,即残差的方差。
AIC赤池信息量准则:$AIC = \frac{1}{d\hat{\sigma}^2}(RSS + 2d\hat{\sigma}^2)$
BIC贝叶斯信息量准则:$BIC = \frac{1}{n}(RSS + log(n)d\hat{\sigma}^2)$
AIC赤池信息量准则2
AIC是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。
通常情况下,AIC定义为:
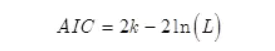
其中k是模型参数个数,L是似然函数。从一组可供选择的模型中选择最佳模型时,通常选择AIC最小的模型。
当两个模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。
一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。
目标是选取AIC最小的模型,AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
BIC贝叶斯信息量准则
BIC(Bayesian InformationCriterion)贝叶斯信息准则与AIC相似,用于模型选择,1978年由Schwarz提出。训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
其中,k为模型参数个数,n为样本数量,L为似然函数。kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
AIC与BIC比较
AIC和BIC的公式中前半部分是一样的,后半部分是惩罚项,当n≥8n≥8时,kln(n)≥2kkln(n)≥2k,所以,BIC相比AIC在大数据量时对模型参数惩罚得更多,导致BIC更倾向于选择参数少的简单模型。
交叉验证:
讨论的对训练误差修正得到测试误差的估计是间接方法,这种方法的桥梁是训练误差,而交叉验证则是对测试误差的直接估计。交叉验证比训练误差修正的优势在于:能够给出测试误差的一个直接估计。在这里只介绍K折交叉验证:我们把训练样本分成K等分,然后用K-1个样本集当做训练集,剩下的一份样本集为验证集去估计由K-1个样本集得到的模型的精度,这个过程重复K次取平均值得到测试误差的一个估计 :
5折交叉验证如下图:(蓝色的是训练集,黄色的是验证集)
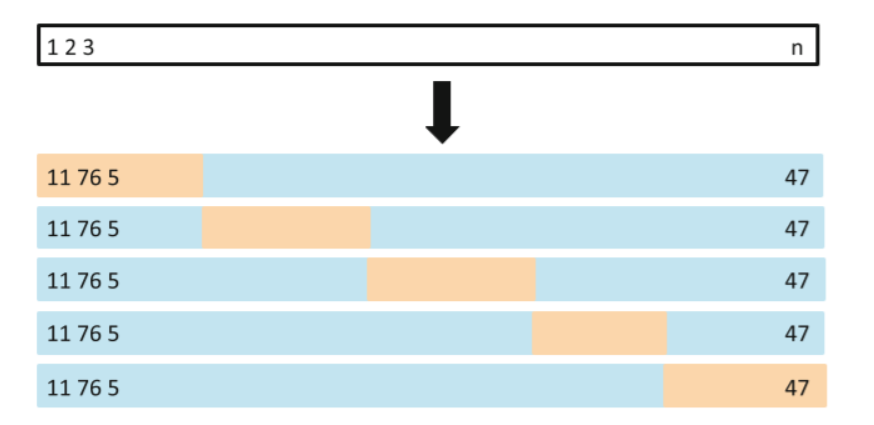
在测试误差能够被合理的估计出来以后,我们做特征选择的目标就是:从p个特征中选择m个特征,使得对应的模型的测试误差的估计最小。对应的方法有:
- 最优子集选择:
- 记不含任何特征的模型为$M_0$,计算这个$M_0$的测试误差。
- 在$M_0$基础上增加一个变量,计算p个模型的RSS,选择RSS最小的模型记作$M_1$,并计算该模型$M_1$的测试误差。
- 再增加变量,计算p-1个模型的RSS,并选择RSS最小的模型记作$M_2$,并计算该模型$M_2$的测试误差。
- 重复以上过程知道拟合的模型有p个特征为止,并选择p+1个模型${M_0,M_1,…,M_p }$中测试误差最小的模型作为最优模型。
向前逐步选择:
最优子集选择虽然在原理上很直观,但是随着数据特征维度p的增加,子集的数量为$2^p$,计算效率非常低下且需要的计算内存也很高,在大数据的背景下显然不适用。因此,我们需要把最优子集选择的运算效率提高,因此向前逐步选择算法的过程如下:
- 记不含任何特征的模型为$M_0$,计算这个$M_0$的测试误差。
- 在$M_0$基础上增加一个变量,计算p个模型的RSS,选择RSS最小的模型记作$M_1$,并计算该模型$M_1$的测试误差。
- 在最小的RSS模型下继续增加一个变量,选择RSS最小的模型记作$M_2$,并计算该模型$M_2$的测试误差。
- 以此类推,重复以上过程知道拟合的模型有p个特征为止,并选择p+1个模型${M_0,M_1,…,M_p }$中测试误差最小的模型作为最优模型。
(d) 压缩估计(正则化):(关于Lasso用于特征提取?)
除了刚刚讨论的直接对特征自身进行选择以外,我们还可以对回归的系数进行约束或者加罚的技巧对p个特征的模型进行拟合,显著降低模型方差,这样也会提高模型的拟合效果。具体来说,就是将回归系数往零的方向压缩,这也就是为什么叫压缩估计的原因了。
岭回归(L2正则化的例子):
线性回归中,我们的损失函数为:
我们在线性回归的损失函数的基础上添加对系数的约束或者惩罚,即:
调节参数$\lambda$的大小是影响压缩估计的关键,$\lambda$越大,惩罚的力度越大,系数则越趋近于0,反之,选择合适的$\lambda$对模型精度来说十分重要。岭回归通过牺牲线性回归的无偏性降低方差,有可能使得模型整体的测试误差较小,提高模型的泛化能力。
- Lasso回归(L1正则化的例子):
回归的一个很显著的特点是:将模型的系数往零的方向压缩,但是岭回归的系数只能呢个趋于0但无法等于0,换句话说,就是无法做特征选择。能否使用压缩估计的思想做到像特征最优子集选择那样提取出重要的特征呢?答案是肯定的!我们只需要对岭回归的优化函数做小小的调整就行了,我们使用系数向量的L1范数替换岭回归中的L2范数:
为什么Losso能做到特征选择而岭回归却不能呢个做到呢?(如图:左边为lasso,右边为岭回归)
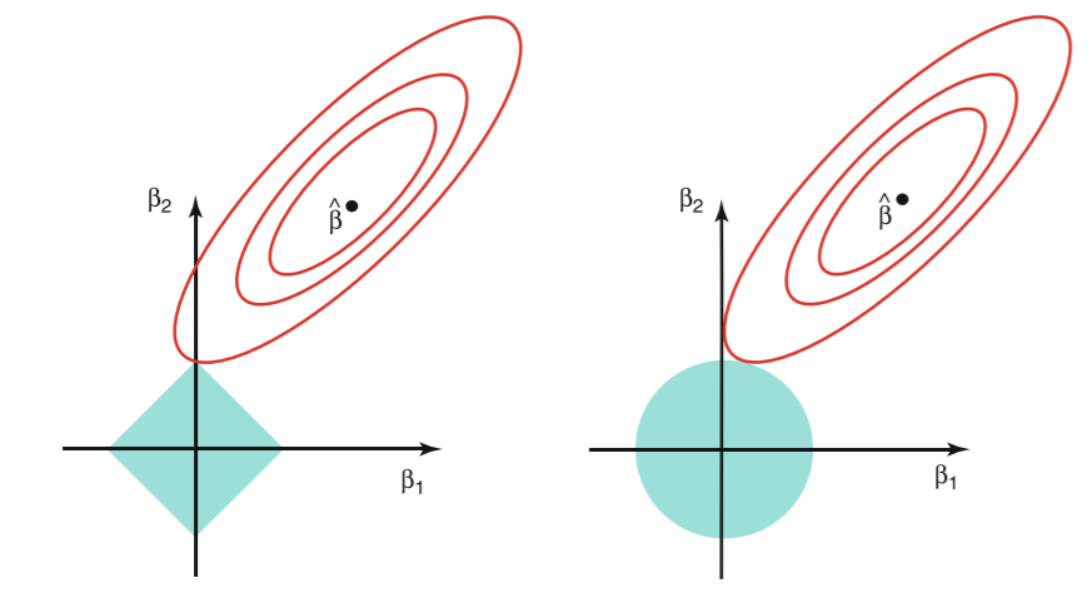
椭圆形曲线为RSS等高线,菱形和圆形区域分别代表了L1和L2约束,Lsaao回归和岭回归都是在约束下的回归,因此最优的参数为椭圆形曲线与菱形和圆形区域相切的点。但是Lasso回归的约束在每个坐标轴上都有拐角,因此当RSS曲线与坐标轴相交时恰好回归系数中的某一个为0,这样就实现了特征提取。反观岭回归的约束是一个圆域,没有尖点,因此与RSS曲线相交的地方一般不会出现在坐标轴上,因此无法让某个特征的系数为0,因此无法做到特征提取。
(e) 降维:
到目前为止,我们所讨论的方法对方差的控制有两种方式:一种是使用原始变量的子集,另一种是将变量系数压缩至零。但是这些方法都是基于原始特征 $x_1,…,x_p$ 得到的,现在我们探讨一类新的方法:将原始的特征空间投影到一个低维的空间实现变量的数量变少,如:将二维的平面投影至一维空间。机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y,其中x是原始数据点的表达,目前最多使用向量表达形式。 y是数据点映射后的低维向量表达,通常y的维度小于x的维度(当然提高维度也是可以的)。f可能是显式的或隐式的、线性的或非线性的。目前大部分降维算法处理向量表达的数据,也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中,包含有冗余信息以及噪音信息,在实际应用例如图像识别中造成了误差,降低了准确率;而通过降维,我们希望减少 冗余信息 所造成的误差,提高识别(或其他应用)的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。在很多算法中,降维算法成为了数据预处理的一部分,如PCA。事实上,有一些算法如果没有降维预处理,其实是很难得到很好的效果的。 (摘自:rosenor1博客)
主成分分析(PCA):
主成分分析的思想:通过最大投影方差 将原始空间进行重构,即由特征相关重构为无关,即落在某个方向上的点(投影)的方差最大。在进行下一步推导之前,我们先把样本均值和样本协方差矩阵推广至矩阵形式:
样本均值Mean:
样本协方差矩阵:
最大投影方差的步骤:
中心化:$ x_i - \bar{x} $
计算每个点
至
方向上的投影:
_计算投影方差:
最大化投影方差求$ \vec{u}_1 $:
得到:
即:
可以看到:$\lambda$为$S^2$的特征值,$u_1$为$S^2$的特征向量。因此我们只需要对中心化后的协方差矩阵进行特征值分解,得到的特征向量即为投影方向。如果需要进行降维,那么只需要取p的前M个特征向量即可。
特征提取的实例:向前逐步回归1
案例来源:https://blog.csdn.net/weixin_44835596/article/details/89763300
根据AIC准则定义向前逐步回归进行变量筛选
AIC简介
AIC即赤池值,是衡量模型拟合优良性和模型复杂性的一种标准,在建立多元线性回归模型时,变量过多,且有不显著的变量时,可以使用AIC准则结合逐步回归进行变量筛选。AICD数学表达式如下:
A I C = 2 p + n ( l o g ( S S E / n ) ) AIC=2p+n(log(SSE/n))
AIC=2p+n(log(SSE/n))
数据获取与处理
1 | import numpy as np |
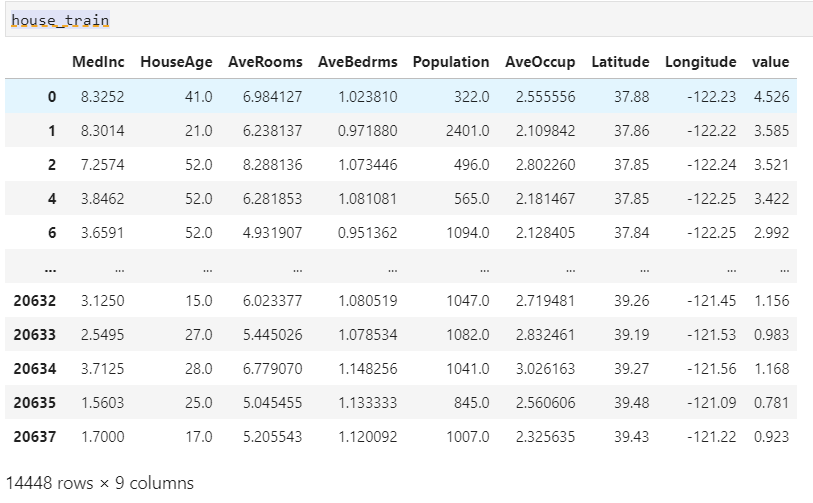
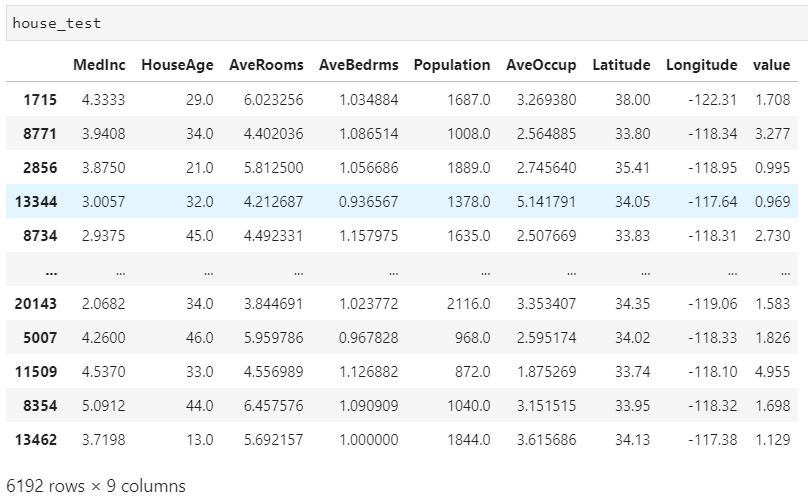
定义向前逐步回归函数
1 | #定义向前逐步回归函数 |
带入数据运行model
1 | forward_select(data=house_train,target="value") |
结果:
aic is 35961.42827917426,continuing!
aic is 34953.4050203734,continuing!
aic is 34719.92315802845,continuing!
aic is 32180.671004119,continuing!
aic is 32049.467078196813,continuing!
aic is 31809.80335748914,continuing!
aic is 31752.599383046603,continuing!
for selection over!
final formula is value~MedInc+HouseAge+Latitude+Longitude+AveBedrms+AveRooms+AveOccup
<statsmodels.regression.linear_model.RegressionResultsWrapper at 0x1907654d188>
1 | lm_1=ols("value~MedInc+HouseAge+Latitude+Longitude+AveBedrms+AveRooms+AveOccup",data=house_train).fit() |
OLS Regression Results
| Dep. Variable: | value | R-squared: | 0.607 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.607 |
| Method: | Least Squares | F-statistic: | 3190. |
| Date: | Sun, 21 Mar 2021 | Prob (F-statistic): | 0.00 |
| Time: | 19:26:28 | Log-Likelihood: | -15868. |
| No. Observations: | 14448 | AIC: | 3.175e+04 |
| Df Residuals: | 14440 | BIC: | 3.181e+04 |
| Df Model: | 7 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>\ | t\ | [0.025 | 0.975] | ||
|---|---|---|---|---|---|---|---|---|
| Intercept | -36.7405 | 0.795 | -46.199 | 0.000 | -38.299 | -35.182 | ||
| MedInc | 0.4427 | 0.005 | 86.003 | 0.000 | 0.433 | 0.453 | ||
| HouseAge | 0.0095 | 0.001 | 18.777 | 0.000 | 0.009 | 0.011 | ||
| Latitude | -0.4187 | 0.009 | -48.104 | 0.000 | -0.436 | -0.402 | ||
| Longitude | -0.4322 | 0.009 | -47.541 | 0.000 | -0.450 | -0.414 | ||
| AveBedrms | 0.6617 | 0.034 | 19.295 | 0.000 | 0.594 | 0.729 | ||
| AveRooms | -0.1187 | 0.007 | -15.986 | 0.000 | -0.133 | -0.104 | ||
| AveOccup | -0.0040 | 0.001 | -7.700 | 0.000 | -0.005 | -0.003 |
| Omnibus: | 3124.833 | Durbin-Watson: | 0.923 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 8914.318 |
| Skew: | 1.138 | Prob(JB): | 0.00 |
| Kurtosis: | 6.102 | Cond. No. | 1.69e+04 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.69e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
可以看到,模型的$R^2$没什么变化,此文章只是一个案例,便于后续遇到较多自变量情况该如何进行筛选。
岭回归实例分享
sklearn.linear_model.ridge_regression(X, y, alpha, *, sample_weight=None, solver=’auto’, max_iter=None, tol=0.001, verbose=0, random_state=None, return_n_iter=False, return_intercept=False, check_input=True)
- 参数:
alpha:较大的值表示更强的正则化。浮点数
sample_weight:样本权重,默认无。
solver:求解方法,{‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’, ‘saga’}, 默认=’auto’。“ svd”使用X的奇异值分解来计算Ridge系数。’cholesky’使用标准的scipy.linalg.solve函数通过dot(XT,X)的Cholesky分解获得封闭形式的解。’sparse_cg’使用scipy.sparse.linalg.cg中的共轭梯度求解器。作为一种迭代算法,对于大规模数据(可能设置tol和max_iter),此求解器比“ Cholesky”更合适。 lsqr”使用专用的正则化最小二乘例程scipy.sparse.linalg.lsqr。它是最快的,并且使用迭代过程。“ sag”使用随机平均梯度下降,“ saga”使用其改进的无偏版本SAGA。两种方法都使用迭代过程,并且当n_samples和n_features都很大时,通常比其他求解器更快。请注意,只有在比例大致相同的要素上才能确保“ sag”和“ saga”快速收敛。您可以使用sklearn.preprocessing中的缩放器对数据进行预处理。最后五个求解器均支持密集和稀疏数据。但是,当fit_intercept为True时,仅’sag’和’sparse_cg’支持稀疏输入。
1 | from sklearn import linear_model |
0.739957023371629
Lasso实例分享
class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=’cyclic’)
- 参数:
alpha:正则化强度,1.0代表标准最小二乘。
fit_intercept:是否计算模型截距。默认true。
normalize:是否标准化,默认false。
positive:是否强制系数为正,默认false。
1 | from sklearn import linear_model |
0.7140164719858566
参考链接
1. https://blog.csdn.net/weixin_44835596/article/details/89763300 ↩
2. https://www.jianshu.com/p/6b8722d5b4f3 ↩