DeepLearning基础
DeepLearning基础
前言
这篇文章主要讲解了深度学习的基础的一些概念,包括神经网络、损失函数等。文中介绍的只是一些基础的,其实还有很多文中并未涉及到的知识点。小编本人在这方面“功力”也不是很深厚,如有错漏,请指正!
背景介绍
1.深度学习应用
图像识别
手机中照片分类-图像分类
NLP(自然语言处理)应用
NLP+图像应用
线性分类器和神经网络
这部分的内容是以图像识别为例子,通过狗、猫、大象的图片识别的具体实例来介绍相应的概念。
线性分类器得分函数
如下图所示,f(x,W)是得分函数,通过输入样本x,以及函数内部的权重W,经由函数映射得到最后图像各分类的得分(或者概率)。
对于图像数据的处理:图像像素是32x32(长X宽),rgb三色通道,是一个三维矩阵,通过一些工具包将三维矩阵拉伸成一个向量。即3072x1,再带入运算。

下面这张图对线性分类器得分函数做了一个简要的图解。下图是三个类别(狗、猫、象)的分类,所以只有三个得分。

损失函数
损失函数,在机器学习里并不少见,简单来说,它用于评估预测结果与正确结果之间的差异。

loss function(损失函数)有不同选择,下面只介绍hinge loss 和 softmax两个损失函数。
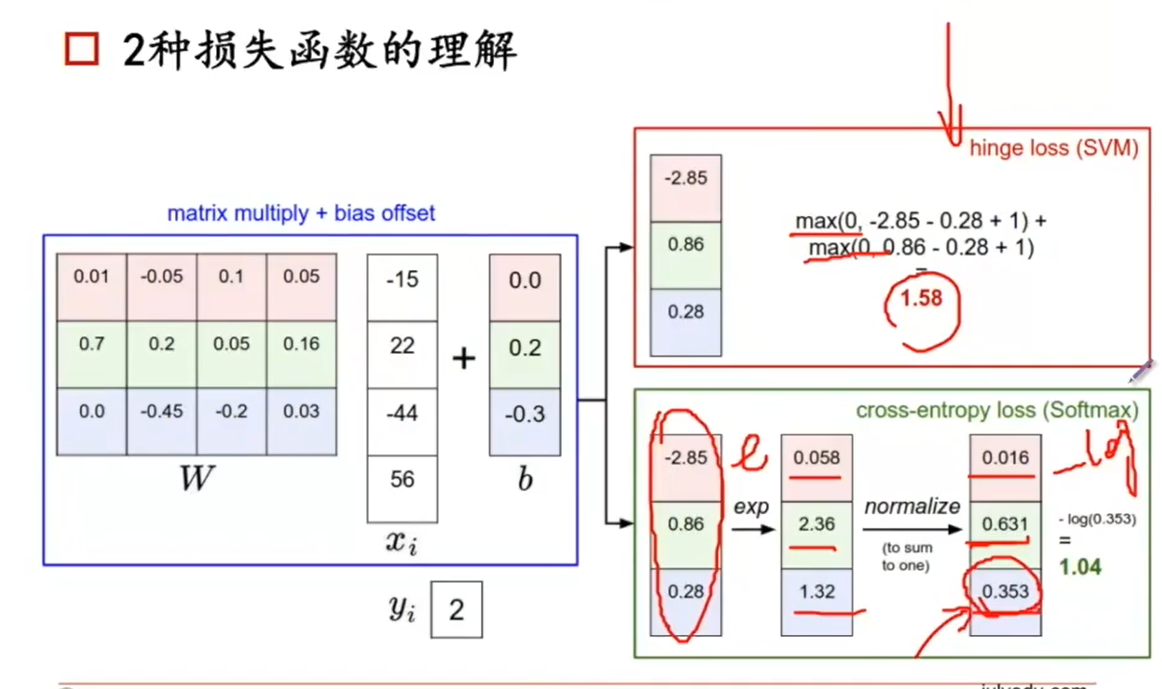
- hinge loss

注:hinge loss 是弱化的,无约束的损失函数。(看看就好)

举个例子,假设图像识别是猫的得分在S2处,那么看你非猫的得分与是猫的得分的距离是否在安全距离(delta为安全距离,上图中红色线段部分)以外,如果是则可以接受,如果不是,那么就会有一个惩罚,惩罚的大小就是:
(非猫的得分 - 最小安全距离)
在安全区之外惩罚为0

红框中公式既是计算的惩罚。
delta是自己设置的,代表你对这个分类器的要求严苛程度,属于超参数。一般设置为固定值1。
- 交叉熵损失函数(softmax分类器)

交叉熵描述的是两个分布间的一个关系。
这个损失函数区别于上面的hinge loss 没有安全距离这个概念,从概率分布的角度来看,一共有【狗🐶、猫🐱、象🐘】三种选项,假设图像是只猫,那么猫的概率为1其他为0,即标准答案为【0,1,0】,再用另外一种方式得到一个概率向量,下面介绍这个所谓的另外一种方式。
已知结果有S1,S2,S3三个score,在此基础上计算对三个score进行处理得到:
对上面的处理得到的值做归一化
可能有人会问,这里为什么要用指数呢?为什么不把他们加在一起除呢?
这是因为得分可能是负值,但是我们希望出来的是一个概率,是一个正数。得到正数后,做一个归一化,即看这个概率有多高。
假设最后通过上面归一化得出来的概率向量是【0.9 0.05 0.5】。
接下来就是求【0 1 0】和【0.9 0.05 0.5】这两个概率向量的差异度有多高,这个时候需要用到交叉熵损失函数,可以从最大似然角度考虑,标准答案是0 1 0,则我们希望的是中间的个概率是最高的。
从log最大似然来考虑,我们希望
可能有人会问,为什么最后取个log?
因为如果不取,概率连乘,概率本身是个很小的值,怕会损失精度(超过计算机计算的精度),所以取个log,相乘就变成了相加,保证了精度。这也是工程上经常会使用的。

在分类问题这里mean square error损失函数(均方差)就不适宜了,因为它是非凸的,非凸函数优化较为麻烦。
至于log的底数,一般以2为底数。
最下面的公式里的C,是为了工程计算方便,加一个常数C稳定幅度。
上面公式中j是代表所有的类别,yi代表第i个类别得分。
下图是带入例子中两种损失函数使用的图解。
神经网络简介
我们可以将神经网络看作一个黑盒子,我们希望通过神经网络这个黑盒子将我们输入的数据进行处理,得到我们想要的结果,如下图所示。

神经网络主要由输入层、隐藏层、输出层、神经元这几个部件组成。
输入层是数据的输入层。隐藏层是对原始数据做一个特征提取,可能是局部特征的抽取,做一个交叉和组合。神经元里则设置了相应的激活函数,对输入的数据进行处理。输出层则是将最后处理的结果进行一个输出。

从逻辑回归到神经元“感知器”
对于逻辑回归,它是一个简单的线性分类器,将输入向量,做一个线性组合得到值z,再通过sigmoid,当z取值非常大,sigmoid近似1,非常小,近似0。他可以把任何连续的值做一个压缩,压缩到0到1之间。这个特性,使得能够将任何连续的值压缩成0-1之间的一个概率值,用法有很多。下图的sita0、sita1、sita2是一个权重(biase)。
sigmoid函数的求导:f‘(x)=f(x)[1-f(x)]

浅层神经网络我们简称为“SNN”,深度神经网络简称为“DNN”。

神经网络非线性能力及原理
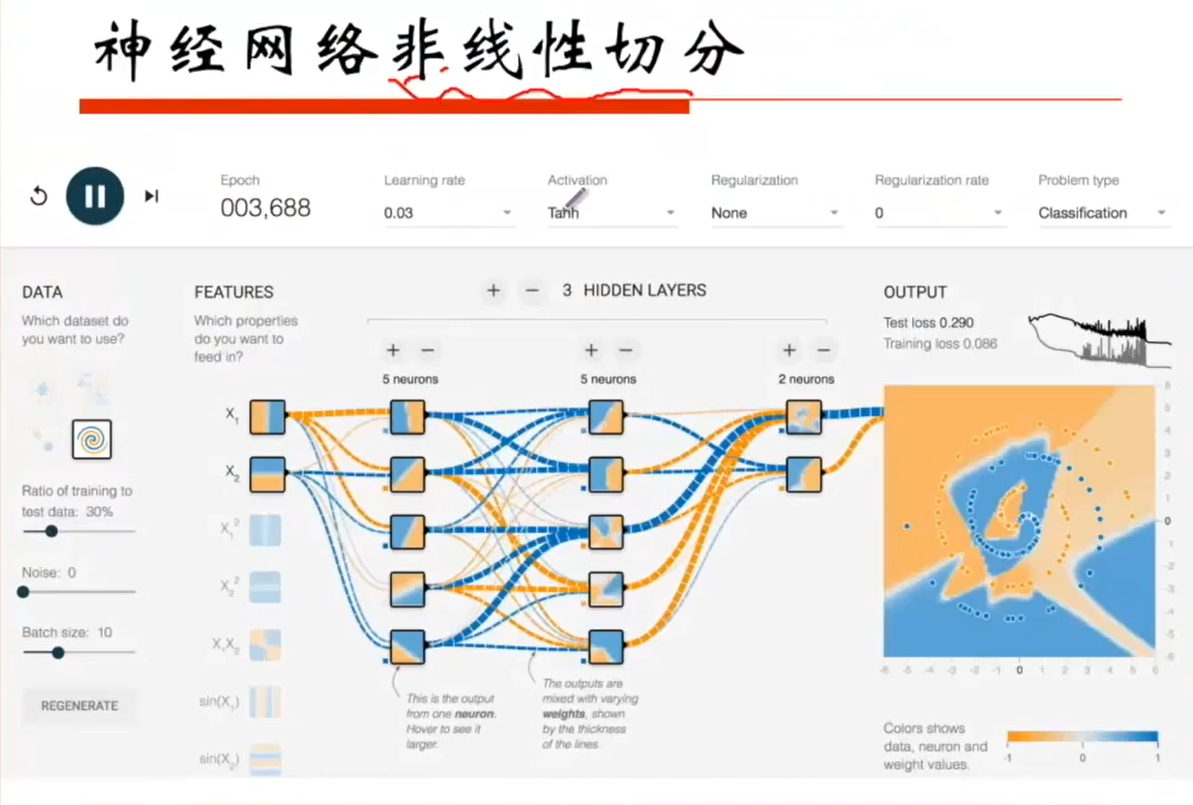
神经网络非线性切分
下面的图片可以发现,数据的分布不是线性的,我们无法用线性的分类器对数据进行划分,那么我们该怎么办呢?
这里就要讲讲关于神经元完成“与”和“或”操作了。
神经网络完成逻辑与
如下图的神经网络,由一层输入层,一层输出层和一些神经元组成。中间黄色圈的神经元激活函数为sigmoid函数,其函数图像如下所示。

假设权重:
假设两个输入x1=x2=0,带入函数如下:
根据上图函数曲线,我们可以看到,x值为-30时,sigmoid函数近似等于0。而当x1和x2取值都为1时,代入sigmoid函数即可得到1,这便达到了逻辑与的效果。具体如下图所示。

再举个例子,可以看到下图,以上图为基础,添加了一层隐藏层,神经元激活函数为sigmoid,这就完成了一个“与”的操作,完成了下图中靠近右侧的平面的非线性的切分。

神经元完成“或”操作
神经元完成“或”操作大体也同上边完成“与”操作类似,不同的地方在于权重的调整。

由上面内容可知,当有and和or操作之后,就可以做各种各样的空间划分。
用线性分类器进行分类,下方为1上方为0代表绿色或非绿色,最后通过AND,即可把区域抠出来。

类似的,把其他绿色的抠出来后,用OR操作,即可把绿色选出来。

单隐层的神经网络可以逼近任何连续函数(只要隐层神经元数够多),找到很多起点终点很接近的小线段做组合,即可组成一个曲线。

工程上,一般取多个隐藏层,每个层少量的神经元。一般简单的分类问题的隐层个数2-3个就好了。
神经网络表达力和过拟合
但是当神经元非常多时,它的表达能力会很强,当它表达能力很强而你又不做控制时,会带来一些问题。比如它强到能够把每一个样本都记下来。

dropput是缓解过拟合的一种正则化手段,这里不做详细介绍。
神经网络结构

神经网络传递函数

在神经网络中,每增加一个隐藏层,就会对输出做一个非线性处理,进行这种处理的函数叫做激活函数。那么为什么需要激活函数呢?
举个例子:
可见结果仍然是一个线性的函数,所以加了一层等于没加。所以需要f(x)
神经网络之Back Propogration算法
反向传播可以获得损失函数最小化的方向,返回的是一个修正值,不会对参数进行更新,参数更新的其中一种方法叫SGD。

如下图,假设O是 output,d是标准答案。

我们会将O和d去做一个差值,用mean square error(用于回归问题),然后往前追溯产生这个误差的根源。在神经网络中这个根源往往是指“w”,即权重。所以需要找到w更新的一个方向。

神经网络之SGD
找误差最小,即对loss函数进行求导,求最小值。神经网络中许多loss函数都是非凸的,很多时候只能找到局部最优,但只要误差在工程应用的允许范围内,我们就可以使用。
这种方法又称为梯度下降。
找到一个梯度后,将第一层和第二层的参数沿着这个梯度做迭代。

回归类的问题用的loss function 都是mean square error,不用边际loss、hinge loss等。loss function=0有两种可能,第一是 loss function 选不对或者定义不对。第二种,中大奖了,不小心找到了最优的一组参数。
假设现在要解决回归类的问题,如下图,黑色字体I1,I2是输入。输入层的蓝色的是权重,最下面的是偏制项,b1 * 1。要求输出是输出层蓝色字体。中间层的红色字体是随机的权重。

下面是进行计算。

可以看到,最后两组的输出为[0.75,0.77],目标输出是[0.01,0.99],通过MSE误差函数进行计算,得到loss值为0.298,后面就是在此基础上修正。
反向传播

由于最后的loss由前面两个函数得到,所以求梯度应该也涉及两个函数。

可以理解为h(g(f(x))),这样求导就相当于三个结果相乘
DeepLearning的基础就介绍到这里,希望大家有所收货!






