字符串知识

字符串简介

字符串：简称为串，是由零个或多个字符组成的有限序列。一般记为s=“a1a2…an”（0<!=∞)。

字符串名称：字符串定义中的s就是字符串的名称。
字符串的值：“a1a2…an”组成的字符序列就是字符串的值，一般用双引号括起来。
字符变量：字符串每一个位置上的元素都是一个字符变量。字符a_i可以是字母、数字或者其他字符。i是该字符在字符串中的位置。
字符串的长度：字符串中字符的数目n称为字符串的长度。
空串：零个字符构成的串也称为「空字符串」，它的长度为0,可以表示为””。
子串：字符串中任意个连续的字符组成的子序列称为该字符串的「子串」。并且有两种特殊子串起始于位置为0、长度为k的子串称为「前缀」。而终止于位置n - 1、长度为k的子串称为「后缀」。
前缀：串s的前缀（prefix）是从s的尾部删除0个或多个符号得到的串。一共有n+1个前缀。
后缀：串s的后缀（suffix）是从s的开始处删除0个或多个符号后得到的串。一共有n+1个后缀。
主串：包含子串的字符串相应的称为「主串」。

举个例子：

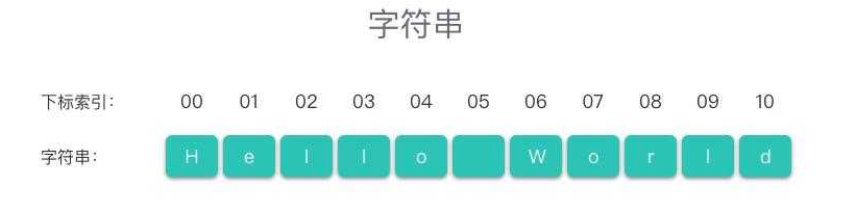
1	str = "Hello World"

在示例代码中，str是一个字符串的变量名称，Hello World 则是该字符串的值，字符串的长度为11。该字符串的表示如下图所示：

根据字符串的特点，我们可以将字符串问题分为以下几种：

字符串匹配问题
- 文本串(T)，模式串(P)，从文本串查找符合P的字串并返回位置
子串相关问题
- 字串中符合某个条件的最大长度
前缀/后缀相关问题
- 给定两个串，求公共前串或公共后串
回文串相关问题
- 字符关于某个位置中间对称。
- 验证回文串，最大回文子串长度
子序列相关问题
- 子序列可以不连续，多段

字符串的比较

字符串的比较操作

两个数字之间很容易比较大小，例如1 < 2。而字符串之间的比较相对来说复杂一点。

字符串之间的大小取决于它们按顺序排列字符的前后顺序。比如字符串str1=”abc”和str2=”acc”,它们的第一个字母都是a，而第二个字母，由于字母b比字母c要靠前，所以b<c，于是我们可以说”abc”<”acd”,也可以说str1 < str2。

字符串之间的比较是通过组成字符串的字符之间的「字符编码」来决定的。而字符编码指的是字符在对应字符集中的序号。

而对于两个长度相等的字符串，我们可以以下面的规则定义两个字符串的大小：

从两个字符串的第0个位置开始，依次比较对应位置上的字符编码大小。
- 如果str1[i]对应的字符编码等于str2[i]对应的字符编码，则比较下一位字符。
- 如果str1[i]对应的字符编码小于str2[i]对应的字符编码，则说明str1 < str2。比如：”abc” < “acc”。
- 如果str1[i]对应的字符编码大于str2[i]对应的字符编码，则说明str1 > str2。比如：”bcd” > “bad”。

而对于两个不相等的字符串，我们可以以下面的规则定义两个字符串的大小：

如果比较到某一个字符串末尾，另一个字符串仍有剩余：
- 如果字符串str1的长度小于字符串str2, 即len(str1) < len(str2)。则str1<str2。比如：”abc”<”abcde”。
- 如果字符串str1的长度大于字符串str2, 即len(str1) > len(str2)。则str1 > str2。比如：”abcde”>”abc”。
- 如果两个字符串每一个位置上的字符对应的字符编码都相等，且长度相同，则说明str1==str2, 比如：”abcd”==”abcd”。

按照上面的规侧，我们可以定义一个strcmp方法，并且规定：

当str1 < str2时，strcmp方法返回-1。
当str1 == str2时，strcmp方法返回0。
当str1 > str2时，strcmp方法返回1。

代码实现：

def strcmp(str1, str2):
	idx1, idx2 = 0, 0
    
    while idx1 < len(str1) and idx2 < len(str2):
        if ord(str[idx1]) == ord(str[idx2]):
            idx1 += 1
            idx2 += 1
        elif ord(str[idx1]) < ord(str[idx2]):
            return -1
        else:
            return 1
    
    if len(str1) < len(str2):
        return -1
    elif len(str1) > len(str2):
        return 1
    else:
        return 0

字符串的字符编码

以计算机中常用字符使用的 ASCII 编码为例。最早的时候，人们制定了一个包含127个字符的编码表 ASCII 到计算机系统中。ASCII 编码表中的字符包含了大小写的英文字母、数字和一些符号。每个字符对应一个编码，比如大写字母A的编码是65,小写字母a的编码是97。后来又针对特殊字符，将 ASCII 扩展到了256位。

ASCII 编码可以解决以英语为主的语言，可是无法满足中文编码。为了解决中文编码，我国制定了GB2312、GBK、GB18030 等中文编码标准，将中文编译进去。但是世界上有上百种语言和文字，各国有各国的标准，就会不可避免的产生冲突，于是就有了Unicode编码。Unicode编码最常用的就是UTF-8编码，UTF-8编码把一个Unicode字符根据不同的数字大小编码成1~6个字节，常用的英文字母被编码成1个字节，汉字通常是3个字节。

字符串的存储结构

字符串的存储结构跟线性表相同，分为「顺序存储结构」和「链式存储结构」。

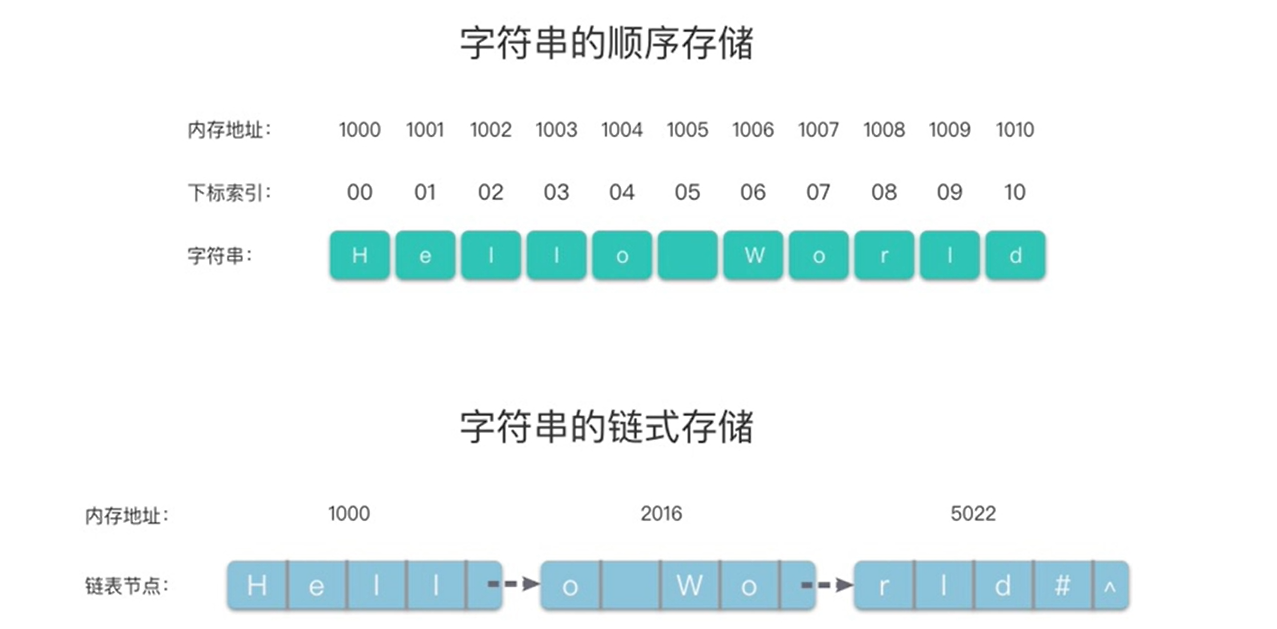
每个链节点可以存放一个或多个字符，通常情况下链节点长度是1或4，为了避免浪费空间。对于没有占满的空间，可以用不属于字符号里的符号进行补齐，这里我们用#。

字符串匹配问题

字符串匹配：又称「模式匹配」。可以简单理解为，给定字符串T和p，在主串T中寻找子串p。主串T又被称为「文本串」，子串p又被称为「模式串」。

在字符串问题中，最重要的问题之一就是字符串匹配问题。而按照模式串的个数，我们可以将字符串匹配问题分为：「单模式串匹配问题」和「多模式串匹配问题」。

单模式串匹配问题

单模式匹配问题：给定一个文本串T=t1t2…tn，再给定一个特定模式串p=p1p2…pn。要求从文本串T找出特定模式串p的所有出现位置。

有很多算法可以解决单模式匹配问题。而根据在文本中搜索模式串方式的不同，我们可以将单模式匹配算法分为以下三种：

基于前缀搜索方法：在搜索窗口内从前向后（沿着文本的正向）逐个读入文本字符，搜索窗口中文本和模式串的最长公共前缀。
- 著名的KMP算法和更快的Shift-Or算法使用的就是这种方法。
基于后缀搜索方法：在搜索窗口内从后向前（沿着文本的反向）逐个读入文本字符，搜索窗口中文本和模式串的最长公共后缀。使用这种搜索算法可以跳过一些文本字符，从而具有亚线性的平均时间复杂度。
- 最著名的BM算法，以及Horspool算法、Sunday算法都使用了这种方法。
基于子串搜索方法：在搜索窗口内从后向前（沿着文本的反向）逐个读入文本字符，搜索满足「既是窗口中文本的后缀，也是模式串的子串」的最长字符串。与后缀搜索方法一样，使用这种搜索方法也具有亚线性的平均时间复杂度。这种方法的主要缺点在于需要识别模式串的所有子串，这是一个非常复杂的问题。
- Rabin-Karp算法、BDM算法、BNDM算法和BOM算法使用的就是这种思想。其中，
  Rabin-Karp算法使用了基于散列的子串搜索算法。

多模式串匹配问题

多模式匹配问题：给定一个文本串T=t_1t_2…t_n，再给定一组模式串P={p^1,p^2,…,p^r}，其中每个模式串p^i是定义在有限字母表上的字符串:

$p^i=p^{i}_{1}p^{i}_{2}…p^{i}_{n}$

要求从文本串T中找到模式串集合P中所有模式串p的所有出现位置。

模式串集合P中的一些字符串可能是集合中其他字符串的子串、前缀、后缀，或者完全相等。解决多模式串匹配问题最简单的方法是利用「单模式串匹配算法」搜索r遍。这将导致预处理阶段的最坏时间复杂度为O(|P|)，搜索阶段的最坏时间复杂度为O(r*n)。

如果使用「单模式串匹配算法」解决多模式匹配问题，那么根据在文本中搜索模式串方式的不同，我们也可以将多模式串匹配算法分为以下三种：

基于前缀搜索方法：搜索从前向后（沿着文本的正向）进行，逐个读入文本字符，使用在$P$上构建的自动机进行识别。对于每个文本位置，计算既是已读入文本的后缀，同时也是$P$中某个模式串的前缀的最长字符串。
- 著名的AC自动机算法、Multiple Shift-And算法使用的这种方法。
基于后缀搜索方法：搜索从后向前（沿着文本的反向）进行，搜索模式串的后缀。根据后缀的下一次出现位置来移动当前文本位置。这种方法可以避免读入所有的文本字符。
- Set Horspool算法、Wu-Manber算法使用了这种方法。
基于子串搜索方法：搜索从后向前（沿着文本的反向）进行，在模式串的长度为min(len(p^i）)的前缀中搜索子串，以此决定当前文本位置的移动。这种方法也可以避免读入所有的文本字符。
- Multiple BNDM算法、SBDM算法、SBOM算法都使用了这种方法。

多模式串匹配算法大多使用了一种基本的数据结构：「字典树（Trie）」。著名的「AC自动机算法」就是在KMP算法的基础上，与「字典树」结构相结合而诞生的。而「AC自动机算法」也是多模式串匹配算法中最有效的算法之一。

所以学习多模式匹配算法，重点是要掌握「字典树」和「AC自动机算法」。

单模式串朴素匹配算法

Brute Force算法：中文意思是暴力匹配算法，也可以叫做朴素匹配算法。

BF算法思想：对于给定文本串T与模式串p，从文本串的第一个字符开始与模式串p的第一个字符进行比较，如果相等，则继续逐个比较后续字符，否则从文本串T的第二个字符起重新和模式串p进行比较。依次类推，直到模式串”中每个字符依次与文本串T的一个连续子串相等，则模式匹配成功，否则模式匹配失败。

BF算法步骤

1.对于给定的文本串T与模式串p，求出文本串T的长度为n，模式串p的长度为m。

2.同时遍历文本串T和模式串p，先将T[0]与p[0]进行比较。

3.如果相等，则继续比较T[1]和p[1]。以此类推，一直到模式串p的末尾p[m一1]为止。

4.如果不相等，则将文本串T移动到上次匹配开始位置的下一个字符位置，模式串p则回退到开始位置，再依次进行比较。

5.当遍历完文本串T或者模式串p的时候停止搜索。

BF算法代码实现

def bruteForce(T:str, p:str) -> int:
    n, m = len(T), len(p)
    # i表示文本串T当前位置，j表示模式串p当前位置
    i, j = 0, 0
    # 当i或j任意一个抵达末尾时停止搜索
    while i < n and j < m:
        # 如果相等则继续匹配下一个字符
        if T[i] == p[j]:
            i += 1
            j += 1
        else:
            # 文本串i下标返回上次匹配的下标位置的下一个位置
            i = i - (j - 1)
            # 模式串j返回到模式串开始位置
            j = 0
    
    if j == m:
        # 匹配成功，返回匹配开始位置的下标
        return i - j
    else:
        # 匹配失败
        return -1

单模式串朴素匹配算法分析

BF算法非常简单，容易理解，但其效率很低。主要是因为在匹配过程中可能会出现回溯：当遇到一对字符不同时，模式串p直接回到开始位置，文本串也回到匹配开始位置的下一个位置，再重新开始比较。

在回溯之后，文本串和模式串中一些部分的比较是没有必要的。由于这种操作策略，导致BF算法的效率很低。最坏情况是每一趟比较都在模式串的最后遇到了字符不匹配的情况，每轮比较需要进行m次字符对比，总共需要进行n-m+1（即匹配到n剩下的长度<m）轮比较，总的比较次数为m*(n-m+1)。所以BF算法的最坏时间复杂度为O(m*n)。

在最理想的情况下（第一次匹配直接匹配成功），BF算法的最佳时间复杂度是O(m)。

在一般情况下，根据等概率原则，平均搜索次数为”(n + m) /2”，所以B「算法的平均时间复杂度为O(n + m)。

单模式串KMP匹配算法

KMP算法：全称叫做「Knuth Morris Pratt算法」，是由它的三位发明者Donald Knuth、
James H.Morris、Vaughan Pratt的名字来命名的。KMP算法是他们三人在I977年联合发表的。

KMP算法思想：对于给定文本串T与模式串p，当发现文本串T的某个字符与模式串p不匹配的时候，可以利用匹配失败后的信息，尽量减少模式串与文本串的匹配次数，避免文本串位置的回退，以达到快速匹配的目的。

朴素匹配算法的缺陷

在朴素匹配算法的匹配过程中，我们分别用指针i和指针j指示文本串T和模式串p中当前正在对比的字符。当发现文本串T的某个字符与模式串p不匹配的时候，j回退到开始位置，i回退到之前匹配开始位置的下一个位置上，然后开启新一轮的匹配，如图所示。

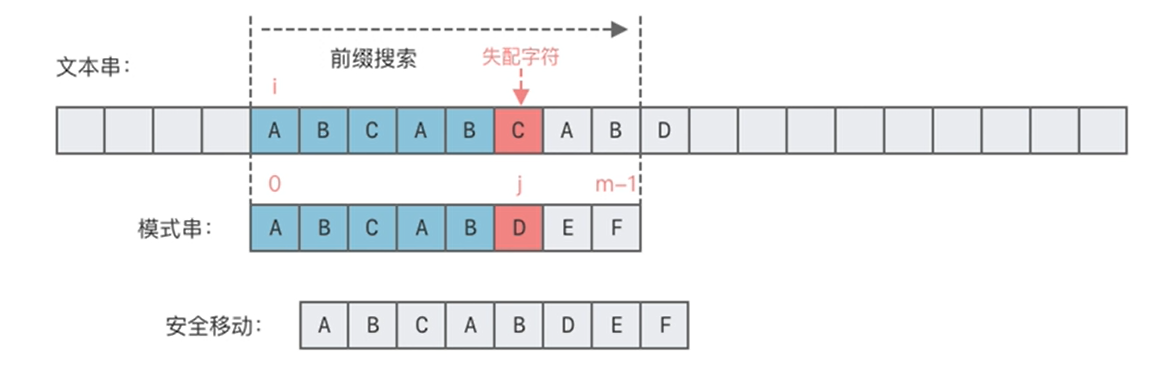
KMP算法的改进点

如果我们可以通过每一次的失配而得到一些「信息」，并且这些「信息」可以帮助我们跳过那些不可能匹配成功的位置，那么我们就能大大减少模式串与文本串的匹配次数，从而达到快速匹配的目的。

每一次失配所告诉我们的信息是：主串的某一个子串等于模式串的某一个前缀。

主串:  [a, e, b, a, c, b, d, a, c, b, a, c] 
				|     |  |
模式串:         [a, c, b, a, c]

字串:[a, c, b] == 模式串前缀: [a, c, b]

这个信息的意思是：如果文本串T[i:i+m]与模式串p的失配是下标位置j上发生的，那么文本串T从下标位置 i 开始连续的 j 个字符，一定与模式串p的前j个字符一模一样，即：T[i:i+j==p[0:j]。

假设模式串是从下标五的位置开始失配的，即前面0~4下标的字串和模式串0~4一致，再加上0~4字串中的3、4与模式串开头两个字符匹配(这里其实是通过预处理模式串获取部分匹配表来得到模式串中前缀和后缀相符的位置)，因此我们可以直接跳到3位置开始匹配，不用像BF算法那样，再接着1~3匹配过来。

KMP算法就是使用了这样的思路，对模式串p进行了预处理，计算出一个「部分匹配表」，用一个数组 next 来记录。然后在每次失配发生时，不回退文本串的指针 i，而是根据「部分匹配表」中模式串失配位置 j 的前一个位置的值，即next[j-1]的值来决定模式串可以向右移动的位数。

比如上述示例中模式串p是在j=5的位置上发生失配的，则说明文本串的子串T[i:i+5]和模式串p[0:5]的字符是一致的，即”ABCAB”==”ABCAB”。而根据「部分匹配表」中next[4]==2,所以不用回退ⅰ，而是将j移动到下标为2的位置，让T[i+5]直接对准p[2],然后继续进行比对。

综上，如果文本串T[i:i+m]与模式串 p 的失配是在第 j 个下标位置发生的，那么：

文本串T从下标位置 i 开始连续的 j 个字符，一定与模式串 p 的前 j 个字符一模一样，即：T[i:i+j]==p[0:j]。
而如果模式串 p 的前 j 个字符中，前k位前缀和后k位后缀相同，即p[0:k]==p[j - k:j]，并且要保证k要尽可能长。

可以推出：文本串子串的后 k 位后缀和模式串子串的前 k 位是相同的，即T[i+m-k:i+m]==p[0:k](这部分是已经比较过的），不需要再比较了，可以直接跳过。

那么我们就可以将文本串中的T[i+m]对准模式串中的p[k], 继续进行对比。这里的k

其实就是next[j-1]。

next数组的构造

我们可以通过递推的方式构造next数组。

我们把模式串p拆分成left、right两部分。left表示前缀串开始所在的下标位置，right表示后缀串开始所在的下标位置，起始时left=0,right=1。
比较一下前缀串和后缀串是否相等。通过比较p[left]和p[right]来进行判断。
如果p[left]!=p[right], 说明当前的前后缀不相同。则让后缀开始位置k不动，前缀串开始位置left不断回退到next[left-1]位置，直到p[left]==p[right]为止。
如果p[left]==p[right], 说明当前的前后缀相同，则可以先让left+=1,此时left既是前缀下一次进行比较的下标位置，又是当前最长前后缀的长度。
记录下标right之前的模式串p中，最长相等前后缀的长度为left，即next[right]=left。

总结，next数组实际上是在找模式串中各个字符所处位置上的前后缀子串中相同的最长子串。

KMP算法整体步骤

1.根据next数组的构造步骤生成「前缀表」next。

2.使用两个指针i、j，其中 i 指向文本串中当前匹配的位置，j 指向模式串中当前匹配的位置。初始时，i=0,j=0。

3.循环判断模式串前缀是否匹配成功，如果模式串前缀匹配不成功，将模式串进行回退，即j=next[j-1],直到j==0时或前缀匹配成功时停止回退。

4.如果当前模式串前缀匹配成功，则令模式串向右移动1位，即 j+=1。

5.如果当前模式串完全匹配成功，则返回模式串p在文本串T中的开始位置，即 i-j+1。

6.如果还未完全匹配成功，则令文本串向右移动1位，即i+=1,然后继续匹配。如果直到文本串遍历完也未完全匹配成功，则说明匹配失败，返回-1.

单模式串KMP算法实现

next数组生成

# 生成next数组
# next[j] 表示下标 j 之前模式串p中，最长相等前后缀长度
def generateNext(p: str):
    m = len(p)
    # 初始化数组元素全为0
    next = [0 for _ in range(m)]
    # left表示前缀串开始所在的下标位置
    left = 0
    # right表示后缀串开始所在的下标位置
    for right in range(1, m):
        while left > 0 and p[left] != p[right]:
            # left进行回退操作
            left = next[left - 1]
        # 匹配成功，找到相同的前后缀，先让left + 1
        if p[left] == p[right]:
            left += 1
        # 记录前缀长度，更新next[right]，结束本次循环
        next[right] = left
    
    return next

KMP算法

# KMP匹配算法，T为文本串，p为模式串
def kmp(T: str, p: str) -> int:
    n, m = len(T), len(p)
    # 生成next数组
    next = generateNext(p)
    # j 为模式串中当前匹配位置
    j = 0
    # i 为文本串中当前匹配位置
    for i in range(n):
        while j > 0 and T[i] != p[j]:
            # 如果模式串匹配不成功，将模式串进行回退, j == 0 时停止
            j = next[j - 1]
        # 当前模式串前缀匹配成功，令 j += 1继续匹配
        if T[i] == p[j]:
            j += 1
        if j == m:
            # 匹配成功返回开始匹配的位置下标
            return i - j + 1
    # 匹配失败，返回 -1
    return -1