哈希表
哈希表
哈希表简介
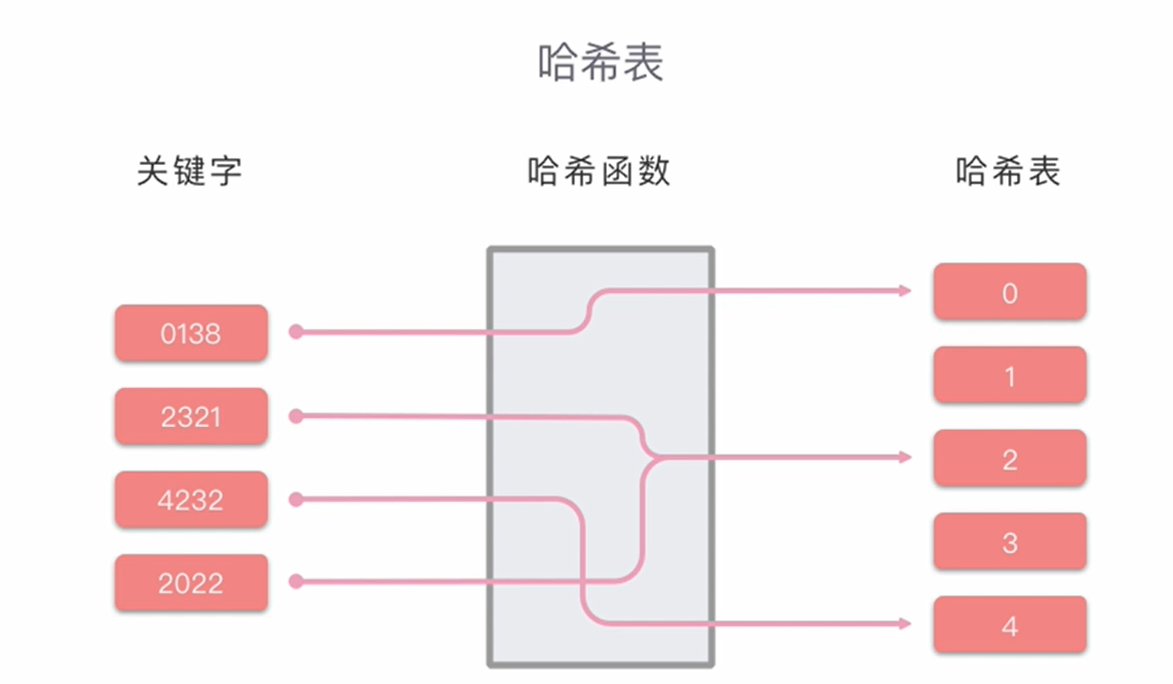
哈希表:也叫做散列表。是根据关键字和值(Key Value)直接进行访问的数据结构。也就是说,它通过关键字key和一个映射函数Hash(key)计算出对应的值value,然后把键值对映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做哈希函数(散列函数),用于存放记录的数组叫做哈希表(散列表)。
哈希表的关键思想是使用哈希函数,将键key和值value映射到对应表的某个区块中。我们可以将算法思想分为两个部分:
- 向哈希表中插入一个关键字:哈希函数决定该关键字的对应值应该存放到表中的哪个区块,并将对应值存放到该区块中。
- 在哈希表中搜索一个关键字:使用相同的哈希函数从哈希表中查找对应的区块,并在特定的区块搜奏该关键字对应的值。
哈希表的原理示意图如下:
哈希函数为:f(x) = x // 1000
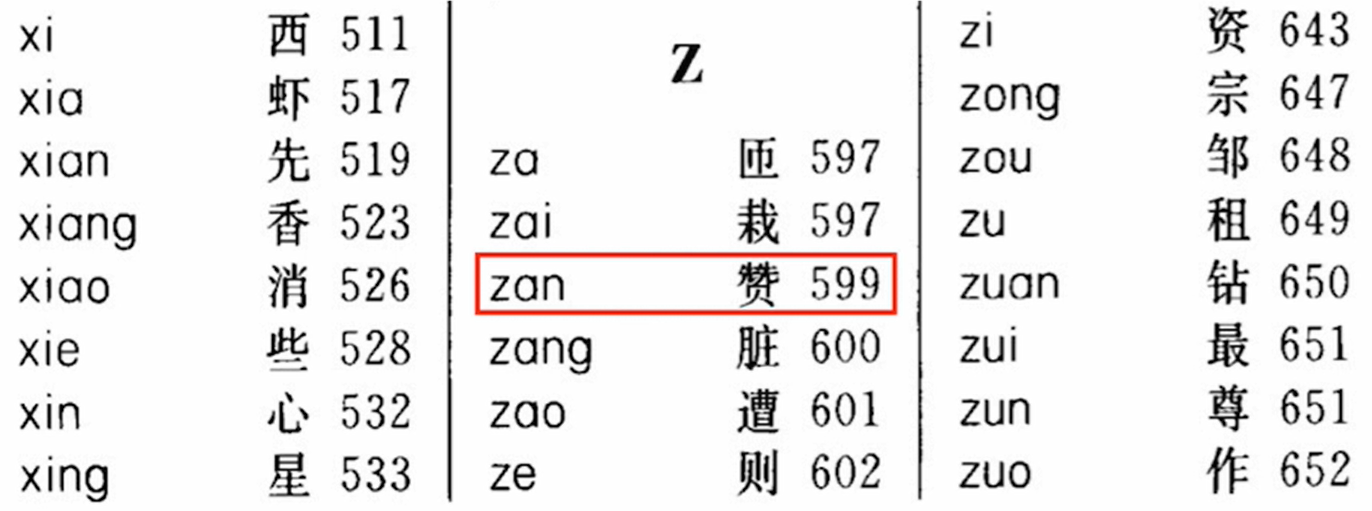
哈希表在生活中的应用也很广泛,其中一个常见例子就是「查字典」
比如为了查找「赞」这个字的具体意思,我们在字典中根据这个字的拼音索引zan,查找到对应的页码为599.然后我们就可以翻到字典的第599页查看「赞」字相关的解释了。
哈希函数
哈希函数:将哈希表中元素的关键键值映射为元素存储位置的函数。
哈希函数是哈希表中最重要的部分。一般来说,哈希函数会满足以下几个条件:
- 哈希函数应该易于计算,并且尽量使计算出来的索引值均匀分布(减少哈希冲突)。
- 哈希函数计算得到的哈希值是一个固定长度的输出值。
- 如果Hash(key1)不等于Hash(key2),那么key1、key2一定不相等。
- 如果Hash(key)等于Hash(key2),那么keyl、key2可能相等,也可能不相等(会发生哈希碰撞)。
在哈希表的实际应用中,关键字的类型除了数字类型,还有可能是字符串类型、浮点数类型、大整数类型,甚至还有可能是几种类型的组合。一般我们会将各种类型的关键字先转换为整数类型,再通过哈希函数,将其映射到哈希表中。
而关于整数类型的关键字,通常用到的哈希函数方法有:直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。
下面我们介绍几个常用的哈希函数方法。
直接定址法
直接定址法:取关键字或者关键字的某个线性函数值为哈希地址。即:Hash(key)=key或者Hash(key)=a*key+b,其中a和b为常数。
这种方法计算最简单,且不会产生冲突。适合于关键字分布基本连续的情况,如果关键字分布不连续,空位较多,则会造成存储空间的浪费。
举一个例子,假设我们有一个记录了从1岁到100岁的人口数字统计表。其中年龄为关键字,哈希函数取关键字自身,如下表所示。

比如,我们想要查询25岁的人有多少,则只要查询表中的第25项即可。
除留余数法
除留余数法:假设哈希表的表长为m,取一个不大于m但接近或等于的质数p,利用取模运算,将关键字转换为哈希地址。即:Hash(key)=key%p,其中p为不大于m的质数。
这也是一种简单且常用的哈希函数方法。其关键点在于p的选择。根据经验而言,一般p取素数或者m,这样可以尽可能的减少冲突。
比如我们需要将7个数[432,5,128,193,92,111,88]存储在11个区块中(长度为11的数组),通过除留余数法将这7个数应分别位于如下地址:

平方取中法
平方取中法:先通过求关键字平方值的方式扩大相近数之间的差别,然后根据表长度取关键字平方值的中间几位数为哈希地址。
比如:Hash(key)=(key*key)//100%1000,先计算平方,去除末尾的2位数,再取中间3位数作为哈希地址。
1443*1443=2082249//100=20822%1000=822
这种方法因为关键字平方值的中间几位数和原关键字的每一位数都相关,所以产生的哈希地址也比较均匀,有利于减少冲突的发生。
基数转换法
基数转换法:将关键字看成另一种进制的数再转换成原来进制的数,然后选其中几位作为哈希地址。
比如,将关键字看做是13进制的数,再将其转变为10进制的数,将其作为哈希地址。
以343246为例,计算方式如下:
$(343246){13} = 3\times13^5 + 4\times13^4 + 3\times13^3 + 2\times13^2 + 4\times13^1 + 6\times13^0 = (1235110){10}$
哈希冲突
哈希冲突:不同的关键字通过同一个哈希函数可能得到同一哈希地址,即key1≠key2,而Hash(key1)=Hash(key2),这种现象称为哈希冲突。
理想状态下,我们的哈希函数是完美的一对一映射,即一个关键字(key)对应一个值(value),不需要处理冲突。但是一般情况下,不同的关键字key可能对应了同一个值vlue,这就发生了哈希冲突。
设计再好的哈希函数也无法完全避免哈希冲突。所以就需要通过一定的方法来解决哈希冲突问题。常用的哈希冲突解决方法主要是两类:「开放地址法」和「链地址法」。
开放地址法
开放地址法:指的是将哈希表中的「空地址」向处理冲突开放。当哈希表未满时,处理冲突时需要尝试另外的单元,直到找到空的单元为止。
当发生冲突时,开放地址法按照下面的方法求得后继哈希地址:H(i)=(Hash(key)+F(i))%m,ⅰ=1,2,3,n(n≤m-1)。(m是哈希表长)
H(i)是在处理冲突中得到的地址序列。即在第1次冲突(i=1)时经过处理得到一个新地址H(1),如果在H(1)处仍然发生冲突,则(ⅰ=2)时经过处理时得到另一个新地址H(2)…。如此下去,直到求得的H(n)不再发生冲突。Hash(key)是哈希函数,m是哈希表表长,取余目的是为了使得到的下一个地址一定落在哈希表中。F(i)是冲突解决方法,取法可以有以下几种:- 线性探测法:$F(i) = 1,2,3,…,m-1$;
- 二次探测法:$F(i) = 1^2, -1^2, 2^2, -2^2, …,n^2(n≤\frac{m}{2})$.
- 伪随机数序列:$F(i)=伪随机数序列$。
案例
举个例子说说明一下如何用以上三种冲突解决方法处理冲突,并得到新地址H(i)。
例如,在长度为11的哈希表中已经填有关键字分别为28、49、18的记录(哈希函数为Hash(key)=key%11)。现在将插入关键字为38的新纪录。根据哈希函数得到的哈希地址为5,产生冲突。接下来分别使用这三种冲突解决方法处理冲突。
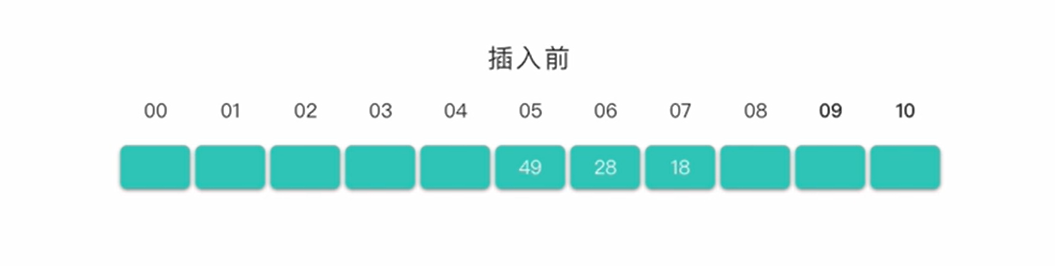
- 使用线性探测法:得到下一个地址
H(1)=(5+1)%11=6,仍然冲突;继续求出H(2)=(5+2)%11=7,仍然冲突;继续求出H(3)=(5+3)%11=8,8对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为8的位置。

- 使用二次探测法:得到下一个地址
H(1)=(5+1*1)%11=6,仍然冲突;继续求出H(2)=(5-1*1)%11=4,4对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为4的位置。(探测当前哈希块前后是否有空块,节省空间)

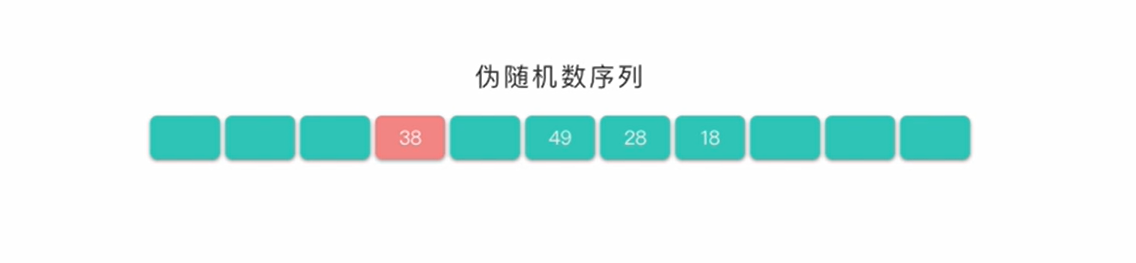
- 使用伪随机数序列:假设伪随机数为9,则得到下一个地址
H(1)=(9+5)%11 =3,3对应的地址为空,处理冲突过程结束,记录填入哈希表中序号为3的位置。
链地址法
链地址法:将具有相同哈希地址的元素(或记录)存储在同一个线性链表中。
链地址法是一种更加常用的哈希冲突解决方法。相比于开放地址法,链地址法更加简单。
我们假设哈希函数产生的哈希地址区间为$[0,m-1]$,哈希表的表长为m。则可以将哈希表定义为一个有m个头节点组成的链表指针数组T。
- 这样在插入关键字的时候,我们只需要通过哈希函数
Hash(key)计算出对应的哈希地址ⅰ,然后将其以链表节点的形式插入到以T[i]为头节点的单链表中。在链表中插入位置可以在表头或表尾,也可以在中间。如果每次插入位置为表头,则插入操作的时间复杂度为O(1)。 - 而在在查询关键字的时候,我们只需要通过哈希函数
Hash(key)计算出对应的哈希地址i,然后将对应位置上的链表整个扫描一遍,比较链表中每个链节点的键值与查询的键值是否一致。查询操作的时间复杂度跟链表的长度k成正比,也就是O(k)。对于哈希地址比较均匀的哈希函数来说,理论上讲,k=n//m,其中n为关键字的个数,m为哈希表的表长。
相对于开放地址法,采用链地址法处理冲突要多占用一些存储空间(主要是链节点占用空间)。但它可以减少在进行插入和查找具有相同哈希地址的关键字的操作过程中的平均查找长度。
这是因为在链地址法中,待比较的关键字都是具有相同哈希地址的元素,而在开放地址法中,待比较的关键字不仅包含具有相同哈希地址的元素,而且还包含哈希地址不相同的元素。
下面我们举个例子来说明如何使用链地址法处理冲突。假设现在要存入的关键字集合keys=[88,60,65,69,90,39,07,06,14,44,52,70,21,45,19,32]。再假定哈希函数为Hash(key)=key%13,哈希表的表长m=13,哈希地址范围为[0,m-1]。将这些关键字使用链地址法处理冲突,并按顺序加入哈希表中(图示为插入链表表尾位置),最终得到的哈希表如下图所示。
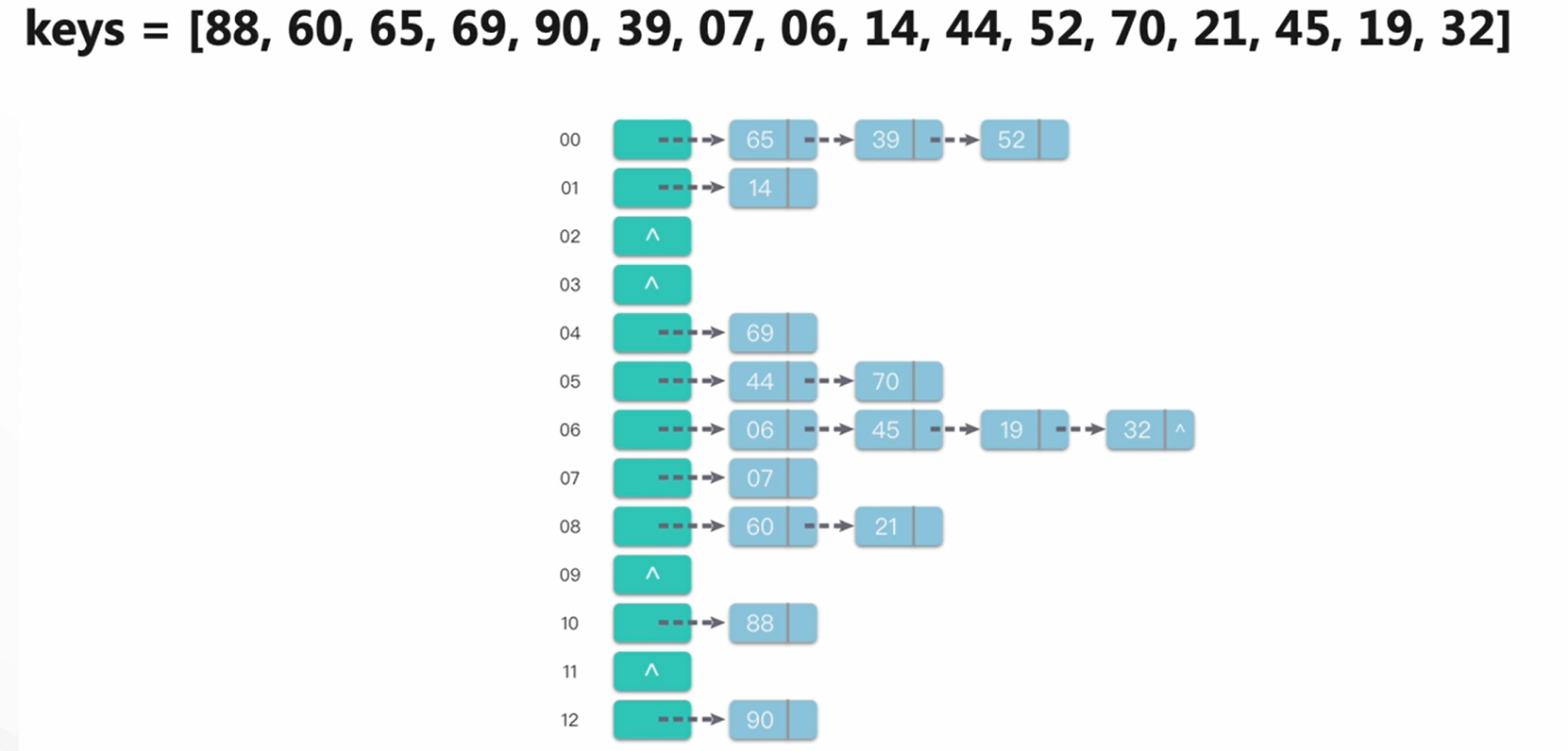
哈希表总结
本文讲解了一些比较基础、偏理论的哈希表知识。包含哈希表的定义,哈希函数、哈希冲突以及哈希冲突的解决方法。
- 哈希表:通过键key和一个映射函数Hash(key)计算出对应的值value,把关键码值映射到表中一个位置来访问记录,以加快查找的速度。
- 哈希函数:将哈希表中元素的关键键值映射为元素存储位置的函数。
- 哈希冲突:不同的关键字通过同一个哈希函数可能得到同一哈希地址。
哈希表的两个核心问题是:「哈希函数的构建」和「哈希冲突的解决方法」。
- 常用的哈希函数方法有:直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。
- 常用的哈希冲突的解决方法有两种:开放地址法和链地址法。
例题
题1:存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
1 | 输入:nums = [1,2,3,1] |
示例 2:
1 | 输入:nums = [1,2,3,4] |
示例 3:
1 | 输入:nums = [1,1,1,3,3,4,3,2,4,2] |
提示:
1 <= nums.length <= 105-109 <= nums[i] <= 109
解题

1 | class Solution: |
题2:有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用
'.'表示。
示例 1:

1 | 输入:board = |
示例 2:
1 | 输入:board = |
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字(1-9)或者'.'
解题

1 | class Solution: |






