向前分步算法

回看Adaboost的算法内容，我们需要通过计算M个基本分类器，每个分类器的错误率、样本权重以及模型权重。我们可以认为：Adaboost每次学习单一分类器以及单一分类器的参数(权重)。接下来，我们抽象出Adaboost算法的整体框架逻辑，构建集成学习的一个非常重要的框架——前向分步算法，有了这个框架，我们不仅可以解决分类问题，也可以解决回归问题。

(1) 加法模型：
在Adaboost模型中，我们把每个基本分类器合成一个复杂分类器的方法是每个基本分类器的加权和，即：

其中：

即基本分类器，$\gamma{m}$ 为基本分类器的参数，$\beta_m$ 为基本分类器的权重，显然这与第二章所学的加法模型十分相似。为什么这么说呢？大家把 $b(x ; \gamma{m})$ 看成是即函数即可。

在给定训练数据以及损失函数 $L(y, f(x))$ 的条件下，学习加法模型$f(x)$就是：

通常这是一个复杂的优化问题，很难通过简单的凸优化的相关知识进行解决。前向分步算法可以用来求解这种方式的问题，它的基本思路是：因为学习的是加法模型，如果从前向后，每一步只优化一个基函数及其系数，逐步逼近目标函数，那么就可以降低优化的复杂度。具体而言，每一步只需要优化：

(2) 前向分步算法：
给定数据集

损失函数 $L(y, f(x))$，基函数集合 ${b(x ; \gamma)}$ ，我们需要输出加法模型$f(x)$。

  • 初始化：$f_{0}(x)=0$

  • 对m = 1,2,…,M:

    • (a) 极小化损失函数：得到参数 $\beta{m}$ 与 $\gamma{m}$

    • (b) 更新：

  • 得到加法模型：

这样，前向分步算法将同时求解从m=1到M的所有参数$\beta{m}$，$\gamma{m}$ 的优化问题简化为逐次求解各个 $\beta{m}$ ，$\gamma{m}$ 的问题。

(3) 前向分步算法与Adaboost的关系：
由于这里不是我们的重点，我们主要阐述这里的结论，不做相关证明，具体的证明见李航老师的《统计学习方法》第八章的3.2节。Adaboost算法是前向分步算法的特例，Adaboost算法是由基本分类器组成的加法模型，损失函数为指数损失函数。

梯度提升决策树(GBDT)

(1) 基于残差学习的提升树算法：

在前面的学习过程中，我们一直讨论的都是分类树，比如Adaboost算法，并没有涉及回归的例子。在上一小节我们提到了一个加法模型+前向分步算法的框架，那能否使用这个框架解决回归的例子呢？答案是肯定的。接下来我们来探讨下如何使用加法模型+前向分步算法的框架实现回归问题。

在使用加法模型+前向分步算法的框架解决问题之前，我们需要首先确定框架内使用的基函数是什么，在这里我们使用决策树分类器。

前面我们已经学过了回归树的基本原理，树算法最重要是寻找最佳的划分点，分类树用纯度来判断最佳划分点使用信息增益（ID3算法），信息增益比（C4.5算法），基尼系数（CART分类树）。但是在回归树中的样本标签是连续数值，可划分点包含了所有特征的所有可取的值。所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。

基函数确定了以后，我们需要确定每次提升的标准是什么。回想Adaboost算法，在Adaboost算法内使用了分类错误率修正样本权重以及计算每个基本分类器的权重，那回归问题没有分类错误率可言，也就没办法在这里的回归问题使用了，因此我们需要另辟蹊径。模仿分类错误率，我们用每个样本的残差表示每次使用基函数预测时没有解决的那部分问题。因此，我们可以得出如下算法：

输入数据集

，输出最终的提升树 $f_{M}(x)$

  • 初始化 $f_0(x) = 0$

  • 对m = 1,2,…,M：

    • 计算每个样本的残差:

      ​

    • 拟合残差$r_{mi}$学习一棵回归树，得到

    • 更新

  • 得到最终的回归问题的提升树：

    下面我们用一个实际的案例来使用这个算法：(案例来源：李航老师《统计学习方法》)
    训练数据如下表，学习这个回归问题的提升树模型，考虑只用树桩作为基函数。

.png)

.png)

.png)

.png)

至此，我们已经能够建立起依靠加法模型+前向分步算法的框架解决回归问题的算法，叫提升树算法。那么，这个算法还是否有提升的空间呢？

(2) 梯度提升决策树算法(GBDT)：

提升树利用加法模型和前向分步算法实现学习的过程，当损失函数为平方损失和指数损失时，每一步优化是相当简单的，也就是我们前面探讨的提升树算法和Adaboost算法。但是对于一般的损失函数而言，往往每一步的优化不是那么容易，针对这一问题，我们得分析问题的本质，也就是是什么导致了在一般损失函数条件下的学习困难。对比以下损失函数：

观察Huber损失函数：

针对上面的问题，Freidman提出了梯度提升算法(gradient boosting)，这是利用最速下降法的近似方法，利用损失函数的负梯度在当前模型的值

作为回归问题提升树算法中的残差的近似值，拟合回归树。与其说负梯度作为残差的近似值，不如说残差是负梯度的一种特例。

以下开始具体介绍梯度提升算法：
输入训练数据集$T=\left{\left(x{1}, y{1}\right),\left(x{2}, y{2}\right), \cdots,\left(x{N}, y{N}\right)\right}, x{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}, y{i} \in \mathcal{Y} \subseteq \mathbf{R}$和损失函数$L(y, f(x))$，输出回归树$\hat{f}(x)$

  • 初始化

    ​

  • 对于m=1,2,…,M：

    • 对i = 1,2,…,N计算：

    • 对 $r{mi}$ 拟合一个回归树，得到第m棵树的叶结点区域 $R{m j}, j=1,2, \cdots, J$

    • 对j=1,2,…J，计算：

      ​

    • 更新

  • 得到回归树：

下面，我们来使用一个具体的案例来说明GBDT是如何运作的(案例来源：https://blog.csdn.net/zpalyq110/article/details/79527653 )：

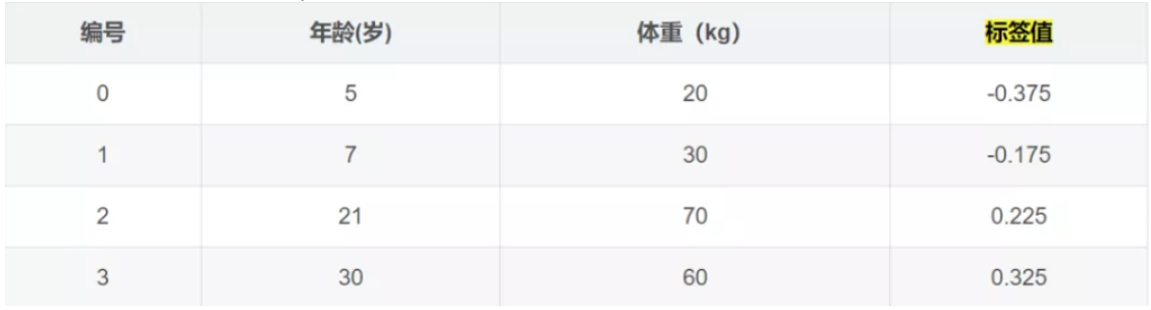
下面的表格是数据：

.png)

学习率：learning_rate=0.1，迭代次数：n_trees=5，树的深度：max_depth=3
平方损失的负梯度为：

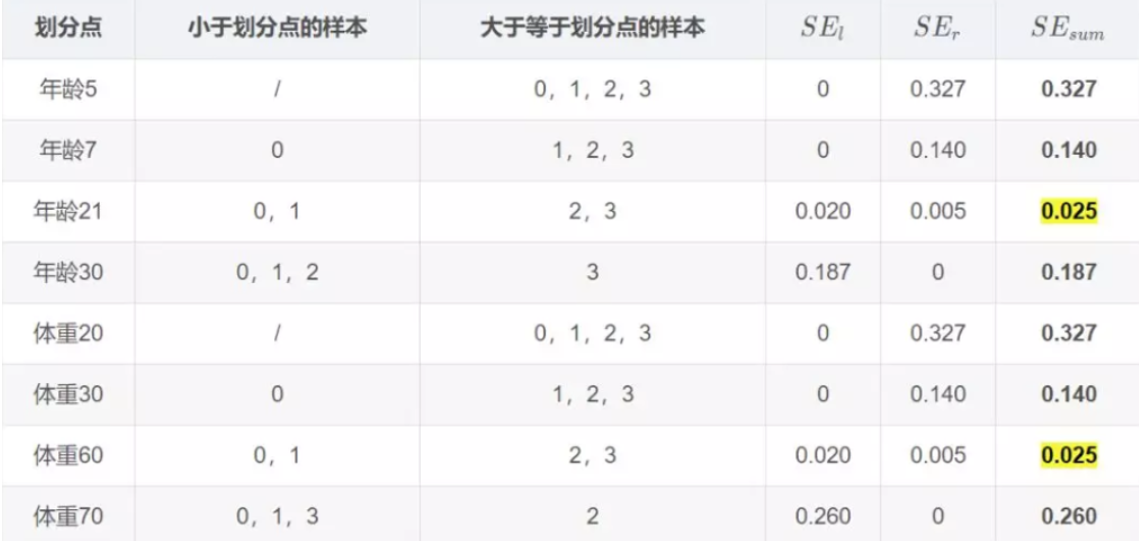
学习决策树，分裂结点：

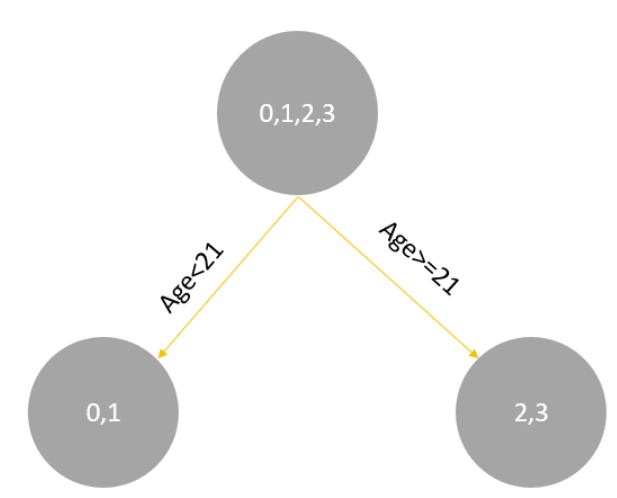
对于左节点，只有0，1两个样本，那么根据下表我们选择年龄7进行划分：

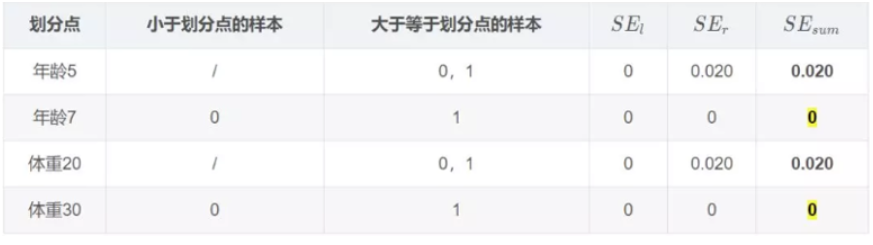
对于右节点，只有2，3两个样本，那么根据下表我们选择年龄30进行划分：

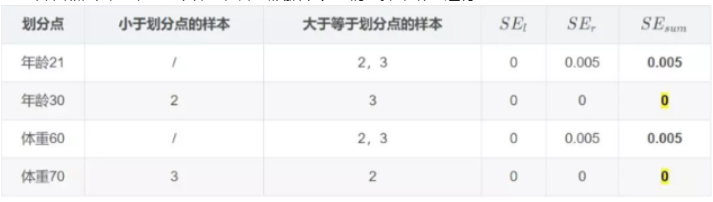
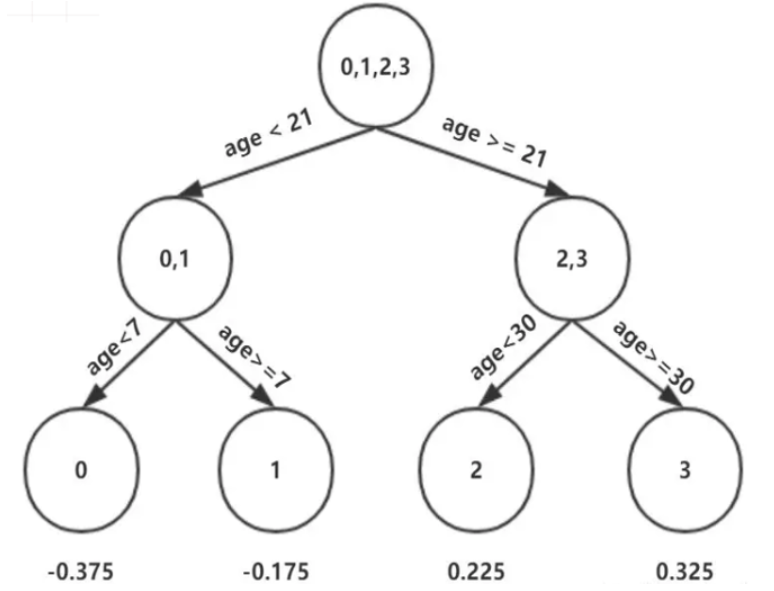
因此根据：

这里其实和上面初始化学习器是一个道理，平方损失，求导，令导数等于零，化简之后得到每个叶子节点的参数$\Upsilon$,其实就是标签值的均值。最后得到五轮迭代：

最后的强学习器为：

预测结果为：

为什么要用学习率呢？这是Shrinkage的思想，如果每次都全部加上（学习率为1）很容易一步学到位导致过拟合。

GBDT案例实践

下面我们来使用sklearn来使用GBDT：
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble.GradientBoostingRegressor

https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html?highlight=gra#sklearn.ensemble.GradientBoostingClassifier

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

'''
GradientBoostingRegressor参数解释：
loss：{‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’：‘ls’ 指最小二乘回归. ‘lad’ (最小绝对偏差) 是仅基于输入变量的顺序信息的高度鲁棒的损失函数。. ‘huber’ 是两者的结合. ‘quantile’允许分位数回归（用于alpha指定分位数）
learning_rate：学习率缩小了每棵树的贡献learning_rate。在learning_rate和n_estimators之间需要权衡。
n_estimators：要执行的提升次数。
subsample：用于拟合各个基础学习者的样本比例。如果小于1.0，则将导致随机梯度增强。subsample与参数n_estimators。选择会导致方差减少和偏差增加。subsample < 1.0
criterion：{'friedman_mse'，'mse'，'mae'}，默认='friedman_mse'：“ mse”是均方误差，“ mae”是平均绝对误差。默认值“ friedman_mse”通常是最好的，因为在某些情况下它可以提供更好的近似值。
min_samples_split：拆分内部节点所需的最少样本数
min_samples_leaf：在叶节点处需要的最小样本数。
min_weight_fraction_leaf：在所有叶节点处（所有输入样本）的权重总和中的最小加权分数。如果未提供sample_weight，则样本的权重相等。
max_depth：各个回归模型的最大深度。最大深度限制了树中节点的数量。调整此参数以获得最佳性能；最佳值取决于输入变量的相互作用。
min_impurity_decrease：如果节点分裂会导致杂质的减少大于或等于该值，则该节点将被分裂。
min_impurity_split：提前停止树木生长的阈值。如果节点的杂质高于阈值，则该节点将分裂
max_features{‘auto’, ‘sqrt’, ‘log2’}，int或float：寻找最佳分割时要考虑的功能数量：

如果为int，则max_features在每个分割处考虑特征。

如果为float，max_features则为小数，并 在每次拆分时考虑要素。int(max_features * n_features)

如果“auto”，则max_features=n_features。

如果是“ sqrt”，则max_features=sqrt(n_features)。

如果为“ log2”，则为max_features=log2(n_features)。

如果没有，则max_features=n_features。
'''

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
    max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))
1
5.009154859960321
1
2
3
4
5
6
7
8
9
from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.score(X_test, y_test)
1
0.432751576681638

与GradientBoostingClassifier函数的各个参数的意思！参考文档：

GradientBoostingRegressor部分参数意思

loss: 选择损失函数，默认值为ls(least squres)

learning_rate: 学习率，模型是0.1

n_estimators: 弱学习器的数目，默认值100

max_depth: 每一个学习器的最大深度，限制回归树的节点数目，默认为3

min_samples_split: 可以划分为内部节点的最小样本数，默认为2

min_samples_leaf: 叶节点所需的最小样本数，默认为1

具体可参考：https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble.GradientBoostingRegressor

GradientBoostingClassifier部分参数意思

min_ samples_split

  • 定义了树中一个节点所需要用来分裂的最少样本数。
  • 可以避免过度拟合(over-fitting)。如果用于分类的样本数太小，模型可能只适用于用来训练的样本的分类，而用较多的样本数则可以避免这个问题。
  • 但是如果设定的值过大，就可能出现欠拟合现象(under-fitting)。因此我们可以用CV值（离散系数）考量调节效果。

min_ samples_leaf

  • 定义了树中终点节点所需要的最少的样本数。
  • 同样，它也可以用来防止过度拟合。
  • 在不均等分类问题中(imbalanced class problems)，一般这个参数需要被设定为较小的值，因为大部分少数类别（minority class）含有的样本都比较小。

min weight fraction_leaf

  • 和上面min samples leaf很像，不同的是这里需要的是一个比例而不是绝对数值：终点节点所需的样本数占总样本数的比值。
  • min samples leaf和min weight fraction_leaf只需要定义一个就行了

max_ depth

  • 定义了树的最大深度。
  • 它也可以控制过度拟合，因为分类树越深就越可能过度拟合。
  • 当然也应该用CV值检验。

max leaf nodes

  • 定义了决定树里最多能有多少个终点节点。
  • 这个属性有可能在上面max_ depth里就被定义了。比如深度为n的二叉树就有最多2^n个终点节点。
  • 如果我们定义了max leaf nodes，GBM就会忽略前面的max_depth。

max_ features

  • 决定了用于分类的特征数，是人为随机定义的。
  • 根据经验一般选择总特征数的平方根就可以工作得很好了，但还是应该用不同的值尝试，最多可以尝试总特征数的30%-40%.
  • 过多的分类特征可能也会导致过度拟合。

参考链接：https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html?highlight=gra#sklearn.ensemble.GradientBoostingClassifier

调参参考博客：https://blog.csdn.net/geduo_feng/article/details/79561571

XGBoost

XGBoost是陈天奇等人开发的一个开源机器学习项目，高效地实现了GBDT算法并进行了算法和工程上的许多改进，被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。

XGBoost本质上还是一个GBDT，但是力争把速度和效率发挥到极致，所以叫X (Extreme) GBoosted，包括前面说过，两者都是boosting方法。XGBoost是一个优化的分布式梯度增强库，旨在实现高效，灵活和便携。 它在Gradient Boosting框架下实现机器学习算法。

XGBoost提供了并行树提升（也称为GBDT，GBM），可以快速准确地解决许多数据科学问题。 相同的代码在主要的分布式环境（Hadoop，SGE，MPI）上运行，并且可以解决超过数十亿个样例的问题。

XGBoost利用了核外计算并且能够使数据科学家在一个主机上处理数亿的样本数据。最终，将这些技术进行结合来做一个端到端的系统以最少的集群系统来扩展到更大的数据集上。Xgboost以CART决策树为子模型，通过Gradient Tree Boosting实现多棵CART树的集成学习，得到最终模型。下面我们来看看XGBoost的最终模型构建：
引用陈天奇的论文，我们的数据为：

1.构造目标函数：

假设有K棵树，则第i个样本的输出为$\hat{y}{i}=\phi\left(\mathrm{x}{i}\right)=\sum{k=1}^{K} f{k}\left(\mathrm{x}{i}\right), \quad f{k} \in \mathcal{F}$，其中，

因此，目标函数的构建为：

其中，

为loss function，

为正则化项。
(2) 叠加式的训练(Additive Training)：

给定样本：

(初始预测)，

…….以此类推，可以得到：

其中，

为前K-1棵树的预测结果，$ f_K(x_i)$ 为第K棵树的预测结果。

因此，目标函数可以分解为：

由于正则化项也可以分解为前K-1棵树的复杂度加第K棵树的复杂度，因此：

由于

在模型构建到第K棵树的时候已经固定，无法改变，因此是一个已知的常数，可以在最优化的时候省去，故：

(3) 使用泰勒级数近似目标函数：

其中，

在这里，我们补充下泰勒级数的相关知识：
在数学中，泰勒级数（英语：Taylor series）用无限项连加式——级数来表示一个函数，这些相加的项由函数在某一点的导数求得。具体的形式如下：

由于$\sum{i=1}^{n}l\left(y{i}, \hat{y}^{(K-1)}\right)$在模型构建到第K棵树的时候已经固定，无法改变，因此是一个已知的常数，可以在最优化的时候省去，故：

  1. 如何定义一棵树

为了说明如何定义一棵树的问题，我们需要定义几个概念：第一个概念是样本所在的节点位置$q(x)$，第二个概念是有哪些样本落在节点j上

，第三个概念是每个结点的预测值 $w{q(x)}$，第四个概念是模型复杂度 $\Omega\left(f{K}\right)$，它可以由叶子节点的个数以及节点函数值来构建，则：

如下图的例子：

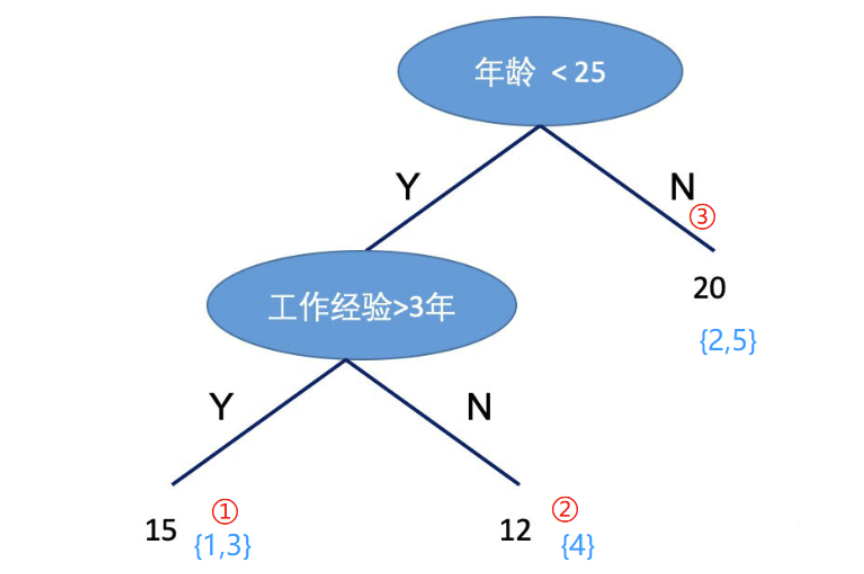
因此，目标函数用以上符号替代后：

由于我们的目标就是最小化目标函数，现在的目标函数化简为一个关于w的二次函数：

根据二次函数求极值的公式：$y=ax^2 bx c$ 求极值，对称轴在 $x=-\frac{b}{2 a}$，极值为 $y=\frac{4 a c-b^{2}}{4 a}$，因此：

以及

5.如何寻找树的形状：

不难发现，刚刚的讨论都是基于树的形状已经确定了计算$w$和$L$，但是实际上我们需要像学习决策树一样找到树的形状。因此，我们借助决策树学习的方式，使用目标函数的变化来作为分裂节点的标准。我们使用一个例子来说明：

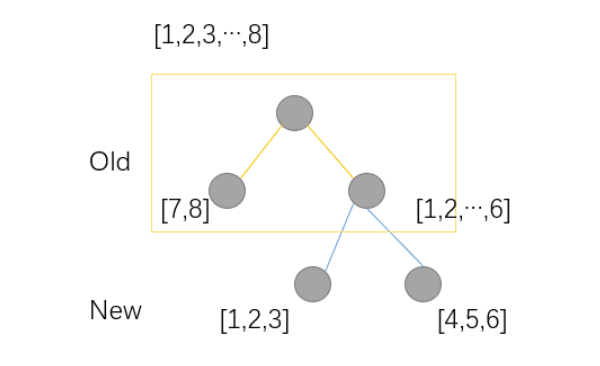
例子中有8个样本，分裂方式如下，因此:

因此，从上面的例子看出：分割节点的标准为

即：

(6.1) 精确贪心分裂算法：

XGBoost在生成新树的过程中，最基本的操作是节点分裂。节点分裂中最重 要的环节是找到最优特征及最优切分点, 然后将叶子节点按照最优特征和最优切 分点进行分裂。

选取最优特征和最优切分点的一种思路如下：首先找到所有的候 选特征及所有的候选切分点, 一一求得其 $\mathcal{L}{\text {split }}$, 然后选择 $\mathcal{L}{\mathrm{split}}$ 最大的特征及 对应切分点作为最优特征和最优切分点。我们称此种方法为精确贪心算法。该算法是一种启发式算法, 因为在节点分裂时只选择当前最优的分裂策略, 而非全局最优的分裂策略。精确贪心算法的计算过程如下所示：

(6.2) 基于直方图的近似算法：

精确贪心算法在选择最优特征和最优切分点时是一种十分有效的方法。它计算了所有特征、所有切分点的收益, 并从中选择了最优的, 从而保证模型能比较好地拟合了训练数据。但是当数据不能完全加载到内存时，精确贪心算法会变得 非常低效，算法在计算过程中需要不断在内存与磁盘之间进行数据交换，这是个非常耗时的过程, 并且在分布式环境中面临同样的问题。为了能够更高效地选 择最优特征及切分点, XGBoost提出一种近似算法来解决该问题。 基于直方图的近似算法的主要思想是：对某一特征寻找最优切分点时，首先对该特征的所有切分点按分位数 (如百分位) 分桶, 得到一个候选切分点集。特征的每一个切分点都可以分到对应的分桶; 然后，对每个桶计算特征统计G和H得到直方图, G为该桶内所有样本一阶特征统计g之和, H为该桶内所有样本二阶特征统计h之和; 最后，选择所有候选特征及候选切分点中对应桶的特征统计收益最大的作为最优特征及最优切分点。基于直方图的近似算法的计算过程如下所示：

1) 对于每个特征 $k=1,2, \cdots, m,$ 按分位数对特征 $k$ 分桶 $\Theta,$ 可得候选切分点,：

2) 对于每个特征 $k=1,2, \cdots, m,$ 有：

3) 类似精确贪心算法，依据梯度统计找到最大增益的候选切分点。

下面用一个例子说明基于直方图的近似算法：

假设有一个年龄特征，其特征的取值为18、19、21、31、36、37、55、57，我们需要使用近似算法找到年龄这个特征的最佳分裂点：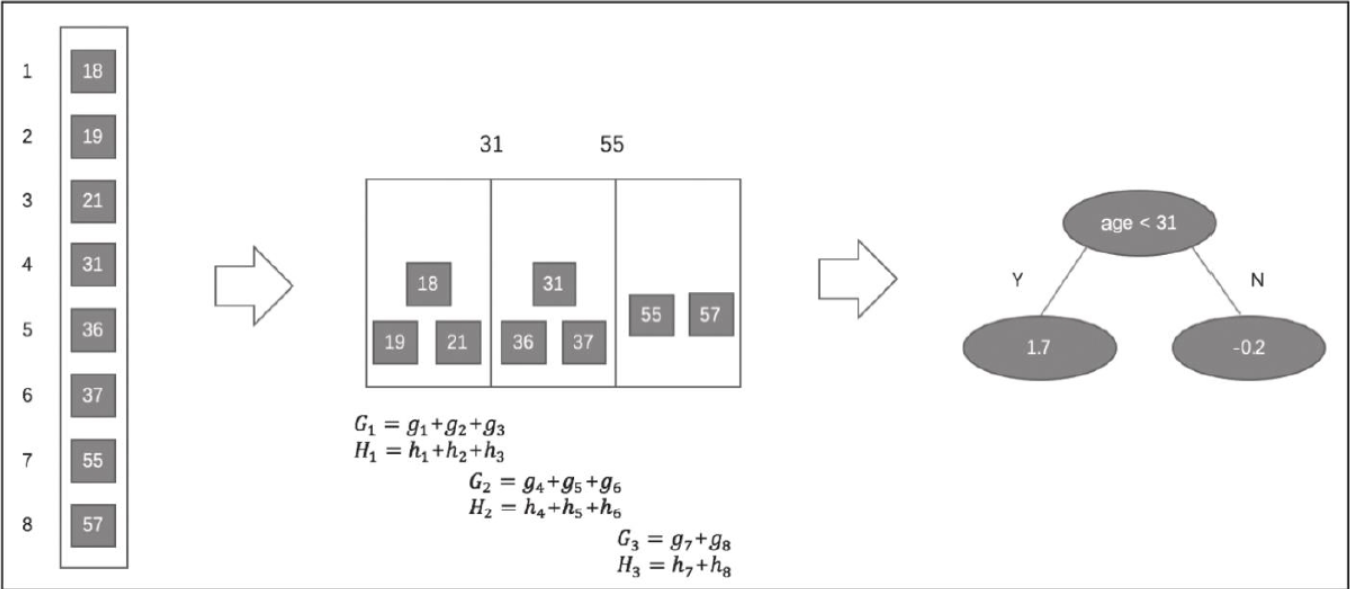

​

近似算法实现了两种候选切分点的构建策略：全局策略和本地策略。全局策略是在树构建的初始阶段对每一个特征确定一个候选切分点的集合, 并在该树每一层的节点分裂中均采用此集合计算收益, 整个过程候选切分点集合不改变。本地策略则是在每一次节点分裂时均重新确定候选切分点。全局策略需要更细的分桶才能达到本地策略的精确度, 但全局策略在选取候选切分点集合时比本地策略更简单。

在XGBoost系统中, 用户可以根据需求自由选择使用精确贪心算法、近似算法全局策略、近似算法本地策略, 算法均可通过参数进行配置。

LightGBM

关于LightGBM的介绍，及它与GBDT、XGBoost的区别笔者之前总结在下面这篇文章里了，感兴趣的小伙伴可以看看：

https://zhuanlan.zhihu.com/p/156041266